Разработка программного комплекса
BURGERS2 для оптимизации и
визуализации вычислительных свойств гибридных разностных схем
А. Бондарев, А. Бондаренко, В. Галактионов, Т. Михайлова, И. Рыжова
Институт прикладной математики им. М.В. Келдыша РАН, Москва, Россия
bond@keldysh.ru, vlgal@gin.keldysh.ru
Оглавление
2. УРАВНЕНИЕ БЮРГЕРСА И ГИБРИДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
3. ПОСТАНОВКА И РЕШЕНИЕ ОПТИМИЗАЦИОННОЙ ЗАДАЧИ
5. ВИЗУАЛИЗАЦИЯ И
ПРИМЕРЫ РАСЧЕТОВ
Аннотация
Данная работа
содержит описание разработанного инструментального программного средства Burgers2, предназначенного для оптимизационной настройки вычислительных
свойств гибридных разностных схем на основе применения уравнения Бюргерса.
Одномерное модельное уравнение Бюргерса, описывающее распространение возмущений
в диссипативной среде, обладает точным решением и широко используется для
настройки и отладки вычислительных инструментов. Программное средство
реализовано на основе решения оптимизационной задачи и визуального
представления результатов. Реализованные в программном комплексе визуальные
представления поверхностей максимальной ошибки и поведения функции ошибки в
выбранный пользователем момент времени позволяют судить о вычислительных
свойствах изучаемой гибридной конечно-разностной схемы. Пользователь обладает
возможностью конструировать гибридные конечно-разностные схемы и исследовать их
свойства на сеточном шаблоне, предоставляемом системой. Визуальное
представление решения оптимизационной задачи позволяет выбирать оптимальные
весовые коэффициенты при построении гибридной конечно-разностной схемы.
Приведены примеры тестовых расчетов.
Ключевые слова: программный комплекс, гибридные разностные схемы, задачи оптимизации, визуализация данных.
Данная работа
посвящена описанию разработанной прототипной версии инструментального
сервисного программного средства Burgers2 (ИСПС Burgers2), предназначенного для проведения оптимизационной настройки и отладки
гибридных разностных схем.
Программный
комплекс Burgers2 основано на численном решении уравнения
Бюргерса и использовании его характерных свойств. Уравнение Бюргерса является
модельным уравнением, описывающим распространение возмущений в диссипативной
среде. Его принято рассматривать как одномерный аналог уравнений Навье-Стокса. Уравнение Бюргерса применяется в различных
областях от вычислительной математики и вычислительной физики до экономических
и социальных задач, то есть всюду, где необходимо моделировать распространение
возмущений в среде с диссипацией.
Характерной
особенностью уравнения Бюргерса является наличие точного решения, выражаемого в
аналитическом виде. Это делает его идеальным объектом для настройки и отладки
вычислительных инструментов – численных методов, разностных схем. Подход
настройки с помощью уравнения Бюргерса вычислительных свойств разностных схем
был предложен в работах [1-3], где рассматривалось влияние счетной вязкости
разностных схем на расчет области высоких градиентов в нестационарных задачах.
Идеология подхода, использованного в [1-3], реализована вычислительно и
программно в данной работе.
Рассматриваемая в
данной работе программная система реализована на основе сочетания решения
оптимизационной задачи и визуального представления результатов. Визуализация
играет в данном случае определяющую роль при анализе пользователем
вычислительных свойств изучаемой конкретной гибридной конечно-разностной схемы.
В программном комплексе реализованы визуальные представления поверхностей
максимальной ошибки и поведения функции ошибки в
выбранный пользователем момент времени. Пользователь обладает возможностью
конструировать гибридные конечно-разностные схемы и исследовать их свойства на
сеточном шаблоне, предоставляемом системой. Визуальное представление решения
оптимизационной задачи позволяет выбирать оптимальные весовые коэффициенты при
построении гибридной конечно-разностной схемы.
2. УРАВНЕНИЕ БЮРГЕРСА И ГИБРИДНЫЕ
РАЗНОСТНЫЕ СХЕМЫ
Рассмотрим краевую задачу, основанную на применении линейного уравнения Бюргерса, представленного в следующем виде:
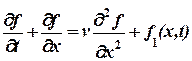(1)
Начальные и граничные условия
представляются в виде:
(2)
,
,
(3)
где 
- точное решение,
описывающее функцию типа бегущей волны.
Точное решение имеет вид
, где 
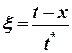(4)
Величины 
и 
характеризуют ширину и
крутизну волны и являются параметрами задачи. Внешний вид точного решения (4)
(бегущей волны) представлен на рисунке
1. Решение представлено на момент времени 
, что соответствует положению волны на середине отрезка 
.
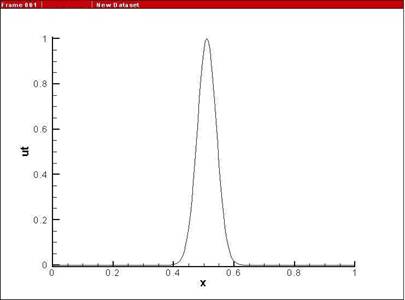
Рис. 1. Точное решение уравнения Бюргерса на момент
времени .
Функция 
в правой части
уравнения (1) является выражением следующего вида:
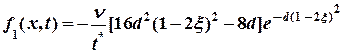(5)
Наличие точного решения позволяет использовать уравнение Бюргерса для построения на его основе программного средства для настройки и отладки вычислительных свойств разностных схем, подобно [1-3].
Для этих целей вычисляется функция 
, представляющая собой модуль процента абсолютной ошибки:
где 
- результат расчета, - точное решение.
Далее ищется 
- максимальное
значение модуля процента абсолютной ошибки во всем диапазоне изменения
аргументов функции. Анализ поведения функции и значения 
позволяет судить о
вычислительных свойствах рассматриваемой конкретной конечно-разностной схемы,
подобно [1-3].
Рассматриваемые в применяемом подходе разностные схемы относятся к классу гибридных разностных схем. Гибридные разностные схемы – это схемы, соединяющие вычислительные свойства различных разностных схем. Подробное описание и классификация различных типов гибридных разностных схем приведены в обзорной работе [4].
Согласно [4], в простейшем случае гибридную схему можно записать как комбинацию:
(6)
где 
– коэффициент гибридности (или весовой коэффициент), 
и 
– разностные схемы,
обладающие различными интересующими исследователя свойствами. Например, – схема первого
порядка точности, а – второго порядка и
т.п. Большинство применяемых для решения практических задач разностных схем
являются гибридными. Согласно [4], к
гибридным схемам относятся такие широко известные алгоритмы, как FCT (flux corrected transport), различные типы TVD (total variation diminishing) разностных схем,
схемы типа ENO (essentially non-oscillatory) и WENO (weighted essentially non-oscillatory) и многие другие. Использование гибридных схем
позволяет исследователю объединять различные разностные схемы в комбинацию,
используя наилучшие свойства каждой из них. В то же время, осуществляя подобное
объединение, необходимо иметь достаточно
четкое представление о свойствах и ограничениях коэффициентов гибридности
(весовых коэффициентов) для того, чтобы используемые свойства разностных схем
соответствовали физической и математической моделям рассматриваемой задачи.
3. ПОСТАНОВКА И РЕШЕНИЕ ОПТИМИЗАЦИОННОЙ
ЗАДАЧИ
Рассмотрим
применение подхода [1-3] к конкретному варианту построения гибридной разностной
схемы. В качестве гибридной разностной схемы использовалась гибридная
разностная схема [3], где в качестве в выражении (6)
используется схема Крэнка-Никольсона, а в качестве - схема Лакса.
Рассмотрим подробно построение разностной схемы [3] в применении к уравнению Бюргерса, записанному в общей форме:
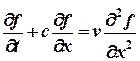(7)
Введем обозначения конечно-разностных операторов для аппроксимации пространственных переменных как
, 
(8)
С помощью
операторов (8) конечно-разностная схема (WW-схема), предложенная в [3], может быть записана для уравнения
(7) с помощью весовых параметров 
и 
следующим образом:
,
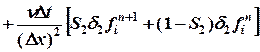(9)
где 
- шаги по времени и
пространственной переменной.
Нетрудно
заметить, что при выборе 
, 
разностная схема (9)
является линейной комбинацией схемы Крэнка-Никольсона, обладающей вторым
порядком точности по времени и пространству, и схемы Лакса, обладающей
существенной искусственной вязкостью. Представив весовой параметр в виде 
, можно записать добавочный член с искусственной вязкостью
как
.
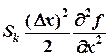(10)
Таким
образом, WW –схема (9)
представляет собой неявную безусловно устойчивую
гибридную схему второго порядка по времени и пространству, обладающую искусственной
вязкостью, позволяющей устранять нефизические осцилляции вблизи разрывов [3].
Управление искусственной вязкостью осуществляется путем выбора весов.
Несомненным достоинством данной разностной схемы является то обстоятельство,
что искусственной вязкостью можно управлять, непосредственно задавая
соответствующее значение весового коэффициента 
.
Данная разностная схема успешно использовалась для решения широкого круга модельных и практических задач вычислительной аэрогазодинамики. Основное достоинство схемы (9) – возможность объединения свойств схемы Крэнка-Никольсона и схемы Лакса.
Схема Крэнка-Никольсона обладает вторым порядком аппроксимации по времени и пространству, обеспечивая тем самым повышенную точность, но в то же время порождает нежелательные осцилляции в области высоких градиентов, уничтожая решение. Схема Лакса имеет первый порядок аппроксимации по времени, «размазывая» решение в области высоких градиентов, но обладает свойством подавлять нежелательные осцилляции.
Целью данного исследования является нахождение таких значений весовых параметров, которые обеспечивали бы достижение повышенной точности (минимальная ошибка), но не допускали бы возникновения осцилляций. Таким образом, уже в постановке задачи заложен конфликт целевых функций.
Для реализации этой цели нужно решать оптимизационную задачу и, следовательно, провести формальную постановку многокритериальной многопараметрической задачи оптимизации, согласно [5].
Оптимизационная задача в данном случае формулируется как поиск следующих величин:
,для всех 
(11)
, так чтобы выполнялось 
.
Здесь 
- количество знакоперемен второй
производной 
. Этот параметр определяет возникновение нежелательных
осцилляций. При их возникновении он начинает неконтролируемо расти. Используя
это свойство, в процессе решения данный параметр постоянно сравнивается с
некоторым эталоном гладкости решения, определяемым пользователем программы с
помощью задания значения параметра 
.
Следует заметить, что данный признак отслеживает начальный момент образования нежелательных осцилляций в решении. Появление осцилляций не означает, что они смогут развиться до степени разрушения решения. Целью применения данного признака является отсечение тех значений исследуемых параметров, где это явление может появиться.
Данная оптимизационная задача решается с помощью применения простого в реализации сеточного метода [5]. Суть этого простого и эффективного метода заключается в сеточном разбиении определяющих параметров оптимизационной задачи (аргументов целевой функции) и вычислении значений целевой функции в каждой точке полученной сетки. Наименьшее из этих значений приближенно принимается за минимум функции во всей области. Ранее традиционно считалось, что для задач большой размерности данный метод непригоден из-за больших вычислительных затрат. Однако современные вычислительные средства позволяют применять его успешно и эффективно, а применение параллельных вычислений позволяет ускорять процессы расчетов на порядки даже при самой безыскусной параллелизации. Это обстоятельство делает самые неприхотливые и простые методы реально применимыми к практическим задачам. Более того, их простота и надежность создают им в этом случае значительные преимущества.
Для рассматриваемой
задачи сеточное разбиение проводится в диапазонах . Для каждой точки сетки вычисляется максимальная ошибка . Каждая точка проверяется на возможное появление осцилляций
с помощью блока-анализатора. Если осцилляции возникают, то эти точки
отбрасываются, путем задания в них заведомо большой отрицательной величины. Как
результат, мы получаем поверхность 
. С помощью полученной поверхности определяется нужный нам
минимум. Сама поверхность представляется визуально в целях контроля решения и
наглядности.
Построение программной реализации описанных в предыдущих разделах алгоритмов проводится по модульному принципу. Общая структура построения приведена в схеме, представленной на рисунке 2.
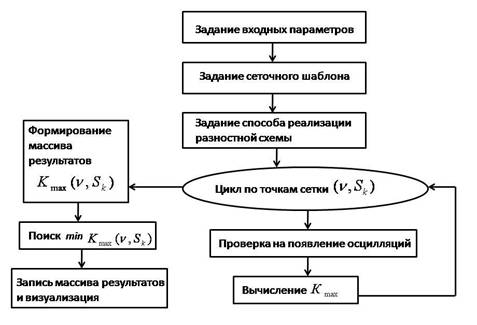
Рис.2. Схема взаимодействия программных модулей.
Сначала в
соответствующем модуле задаются входные параметры оптимизационной задачи и,
таким образом, проводится сеточное разбиение определяющих параметров. В
качестве входных параметров служат: 
– число точек по 
, значения 
и 
, 
– число точек
разбиения отрезка 
, значения 
и 
, 
- число точек разбиения отрезка 
, а также величины и , описывающие бегущую волну в точном решении.
Задание сеточного шаблона проводится в отдельном программном модуле. Это сделано для того, чтобы повысить гибкость программного средства, т.к. построение гибридной схемы может проводиться не только по простейшему принципу (6), но и с использованием более сложной линейной комбинации.
Реализация конечно-разностной схемы предусмотрена в соответствующем модуле, как для явных, так и для неявных схем. Неявные схемы реализуются с помощью скалярной прогонки.
Далее
реализуется цикл по точкам сетки 
. Для каждого фиксированного набора значений проводится решение
уравнения Бюргерса с помощью рассматриваемой разностной схемы. Решение
проверяется на наличие нежелательных и неконтролируемых осцилляций. Проводится
сравнение с точным решением и вычисляется значение . Таким образом формируется искомый
массив результатов и проводится поиск
положительного минимума данного массива.
Вывод данных осуществляется
на экран и в текстовый файл. Полученные результаты позволяют для каждого фиксированного значения 
определить значение
минимума максимальной ошибки и соответствующее
значение 
. Отрицательное значение максимальной ошибки свидетельствует
о наличии нежелательных осцилляций. Пример полученных в расчете результатов
представлен на таблице 1.
Таблица 1.
|
|
|
|
|
1.000000E-03 |
2.761018 |
8.000001E-01 |
|
2.000000E-03 |
1.280981 |
3.000000E-01 |
|
3.000000E-03 |
4.440367E-01 |
1.000000E-01 |
|
4.000000E-03 |
-1.000000 |
9.000001E-01 |
|
5.000000E-03 |
5.271882E-01 |
1.000000E-01 |
|
6.000000E-03 |
7.957876E-01 |
1.000000E-01 |
|
7.000000E-03 |
1.002550 |
1.000000E-01 |
|
8.000000E-03 |
1.165241 |
1.000000E-01 |
|
9.000000E-03 |
1.295036 |
1.000000E-01 |
|
1.000000E-02 |
1.401329 |
1.000000E-01 |
5.
ВИЗУАЛИЗАЦИЯ И ПРИМЕРЫ РАСЧЕТОВ
Визуальное
представление данных, полученных в результате решения оптимизационной задачи,
играет ключевую роль при выборе пользователем оптимальных весовых коэффициентов
для рассматриваемой гибридной конечно-разностной схемы. Фиксирован основной тип
визуального представления решения оптимизационной задачи – представление в виде поверхности.
Следует заметить, что вместо параметров и 
могут рассматриваться
любые два параметра 
и 
рассматриваемой
задачи, по которым задается сеточное разбиение, и, соответственно, функция 
.
Также
пользователь обладает возможностью рассмотреть поведение функции ошибки в любой выбранной
точке сеточного разбиения оптимизационной задачи в любой фиксированный момент
времени.
Программный комплекс реализует соответствующую конвертацию данных в нужные форматы для подключения универсальных систем визуализации научных данных, таких как TecPlot, ParaView, VisIt 2.0.
Основываясь на этих двух основных типах визуального представления, пользователь обладает возможностью принять решение о пригодности или непригодности рассматриваемой гибридной конечно-разностной схемы для достижения поставленных целей. Далее с помощью визуального представления поверхности максимальной ошибки пользователь может отбросить те области сеточного разбиения, где возникают нежелательные осцилляции, разрушающие решение, и выбрать весовые коэффициенты для конструируемой гибридной конечно-разностной схемы, доставляющие минимум функции максимальной ошибки.
С помощью разработанного инструментального программного средства был проведен ряд расчетов для различных разностных схем и шаблонов. Ниже приведены два характерных примера результатов подобных расчетов.
В первом
примере использовался сеточный шаблон (9) с выбором весовых коэффициентов , , обеспечивающий гибрид схем Лакса и Крэнка-Никольсона. На рисунке
3 приведен вид поверхности абсолютной ошибки. Область отрицательных данных
отмечает места появления осцилляций.
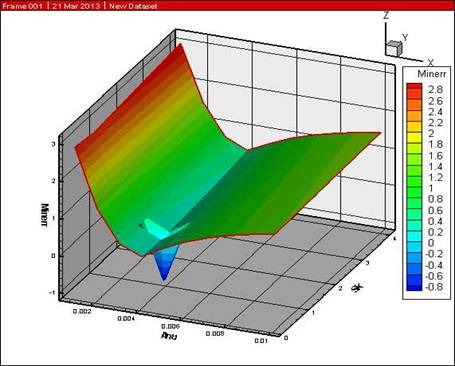
Рис. 3. Поверхность абсолютной ошибки при выборе
весовых коэффициентов ,
С помощью
полученных данных для любого значения легко подобрать
значение весового коэффициента , обеспечивающее минимальную ошибку, а, следовательно,
максимальную точность рассматриваемой гибридной разностной схемы. Естественно,
при подобной процедуре области нежелательных осцилляций изымаются из
рассмотрения.
Практический принцип отбора весового коэффициента при возникновении
признаков начала появления нежелательный осцилляций представлен на рисунке 4,
где представлена проекция поверхности абсолютной ошибки на плоскость . При срабатывании признака появления нежелательных
осцилляций для любого значения , находящегося в диапазоне зоны осцилляций (между
вертикальными пунктирными линиями на рисунке 4), выбирается максимальное
значение весового коэффициента из диапазона,
определяемого размерами зоны появления осцилляций (горизонтальная пунктирная
линия на рисунке 4). Такой
принцип отбора применяется для того, чтобы гарантированно отсекать области
значений весового коэффициента , где могут возникать осцилляции.
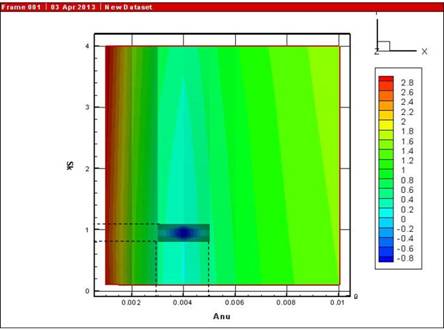
Рис. 4. Организация выбора весового коэффициента при
появлении признаков нежелательных осцилляций.
Одновременно для любой фиксированной пары значений пользователь обладает
возможностью детально рассмотреть поведение функции ошибки в любой выбранный
момент времени. На рисунке 5 представлено поведение функции ошибки при
и 
на
момент времени , что соответствует положению волны на середине отрезка . Из рисунка 5 можно сделать вывод о том, что максимальная
ошибка в данном случае
составляет около 0.5 %.
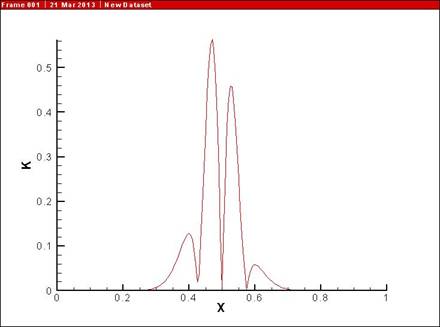
Рис. 5.
Визуальное представление функции ошибки
при выборе весов , .
Второй пример
рассматривает также шаблон (9) при выборе весовых коэффициентов , 
. Такой выбор весовых коэффициентов подразумевает отказ от
использования второго порядка аппроксимации по времени и переход к схеме
первого порядка. Вид поверхности абсолютной ошибки приведен на рисунке 6.
Данный рисунок дает точное представление об изменении поведения абсолютной ошибки при переходе к разностной схеме первого порядка аппроксимации по времени. Меняется структура поверхности, значение ошибки резко увеличивается во всем поле определяющих параметров. Однако при подобном переходе к значительно более грубой конечно-разностной схеме нежелательных осцилляций не возникает.
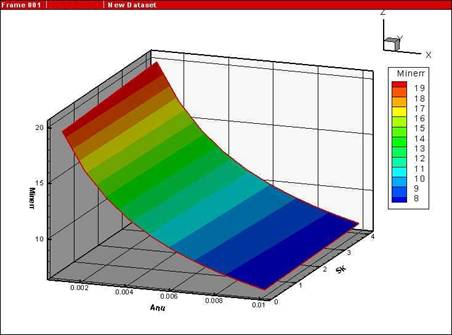
Рис. 6. Поверхность абсолютной ошибки при выборе
весовых коэффициентов , .
Аналогично
предыдущему примеру расчетов на рисунке 7 представлено распределение функции ошибки при тех же значениях
параметров и на момент времени .
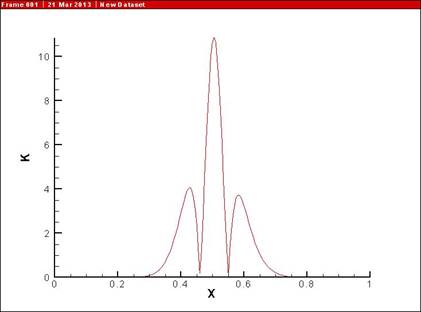
Рис. 7.
Визуальное представление функции ошибки
при выборе весов , .
Рисунок 7
показывает, что при отказе о второго
порядка аппроксимации максимальная ошибка возрастает более чем
на порядок и составляет в данном случае более 10 %.
Программа Burgers2 реализована на языке Fortran90. Данная версия является прототипной и разработана для реализации алгоритма. В дальнейшем данная версия нуждается в создании интерфейса, ориентированного на конечного пользователя и обеспечивающего:
- расширение возможностей работы с сеточным шаблоном, обеспечивающих конструирование гибридных конечно-разностных схем;
- удобную организацию ввода-вывода данных;
- сопряжение с внешними устройствами;
- автоматическую конвертацию данных в основные форматы, используемые в универсальных системах визуального представления научных данных.
Также следует заметить, что решение рассматриваемой оптимизационной задачи реализовано в текущем варианте программы с использованием последовательного алгоритма. Однако здесь возможна организация надстройки для проведения параллельных вычислений для наборов определяющих параметров вместо реализации цикла по точкам сетки. Подобный подход к решению оптимизационной задачи был предложен и опробован в работе [6].
Разработана прототипная версия
инструментального сервисного программного средства Burgers2, предназначенного для проведения оптимизационной
настройки и отладки гибридных разностных схем. Программное средство позволяет
отлаживать вычислительные свойства гибридных разностных схем на модельном
уравнении Бюргерса, описывающем распространение возмущений в диссипативной
среде. Основой алгоритма является сочетание решения оптимизационной задачи и
визуального представления результатов. Данная программная система может служить
инструментом отладки и настройки вычислительных свойств разностных схем, а
также использоваться для образовательных целей, будучи наглядным средством
визуальной демонстрации вычислительных свойств
конечно-разностных схем, используемых в задачах математического
моделирования. Дальнейшее развитие
данной прототипной программной системы предполагается в направлении создания
интерфейса, ориентированного на конечного пользователя, и разработки данного
программного средства в варианте, предназначенном для проведения параллельных
расчетов.
Данная работа выполнена при поддержке
Российского фонда фундаментальных исследований (грант 13-01-00367).
ЛИТЕРАТУРА
[1] Русаков С.В. Влияние счетной вязкости некоторых разностных схем на расчет области высоких градиентов в нестационарных задачах / Численные методы в аэродинамике:сб.трудов. М:.Изд.МГУ. 1980. вып.4. С.58-67.
[2] Русаков С.В. О некотором классе схем повышенного порядка точности по пространственным переменным / Численные методы в аэродинамике:сб.трудов. М:.Изд.МГУ. 1980. вып.5. С.3-13.
[3] Бондарев А.Е. Численное решение уравнения Бюргерса в области высоких градиентов // Препринты ИПМ им.М.В.Келдыша. 1990. № 12. 13 с.
[4] Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001, 608 с.
[5] Штойер
Р. Многокритериальная оптимизация. Теория, вычисления и приложения. М.: Радио и связь. 1992. 504 с.
[6] Бондарев А.Е. Решение задачи оптимизационного анализа с помощью параллельных вычислений // Новые информационные технологии в автоматизированных системах: материалы пятнадцатого научно-практического семинара. М.:МГИЭМ. 2012. С. 89-93.
Design of Program Tool Burgers2 for Hybrid Finite
Diference Schemes Optimization and Visualization
Bondarev A., Bondarenko A., Galaktionov
V., Mihailova T., Ryzhova
I.
Keldysh Institute of Applied Mathematics RAS
bond@keldysh.ru,
vlgal@gin.keldysh.ru
Abstract
The paper contains the description of
developed program tool Burgers2. This
program tool is intended for tuning and optimization of computational
properties for hybrid finite-difference schemes applied to Burgers equation.
One-dimensional model Burgers equation describes propagation of disturbances
for dissipative medium. The equation has exact solution, so it is widely used
for tuning-up of computational tools. Described program tool is based on
combining of optimization problem solution and visual data presentation. Visual
presentations of maximal error surface and error function are implemented as
program tool features. User is able to visualize error function distribution
for any chosen moment of time. These visual presentations allow analyzing and
control computational properties of hybrid finite-difference schemes under
consideration. Users have possibility of creating hybrid finite-difference
schemes and analyzing computational properties for chosen grid template
provided by program tool. Visual presentation of optimization problem solution
allows finding of suitable weight coefficients for hybrid finite-difference scheme
under consideration. The examples of test calculations are included.
Key words: program tool, hybrid finite-difference schemes, optimization problem,
data visualization.
References
1. Rusakov S.V. Vliyanie schetnoy vyazkosti nekotorykh raznostnykh skhem na
raschet oblasti vysokikh gradientov v nestatsionarnykh zadachakh [Numerical
viscosity influence in high-gradient field for specific finite-difference
schemes applied to unsteady problems]. CHislennye metody v aerodinamike:sb.trudov
[Numerical methods in aerodynamics], Moscow University, 1980, N 4, p.58-67. (in
Russ.)
2. Rusakov S.V. O nekotorom klasse skhem povyshennogo
poryadka tochnosti po prostranstvennym peremennym [On specific class of finite-difference schemes
with high-order accuracy for space variables]. CHislennye metody v aerodinamike:sb.trudov [Numerical methods in aerodynamics],
Moscow University, 1980, N 5, p.3-13. (In Russian).
3.
Bondarev A.E. CHislennoe reshenie uravneniya Byurgersa v oblasti vysokikh gradientov [Numerical
solving of Burgers equation for high-gradient region]. Preprinty IPM im.M.V.Keldysha
[Keldysh Institute of Applied Mathematics Preprint],
1990, N 13. (In Russian).
4. Kulukovsky A.G., Pogorelov N.V.,
Semenov A.Yu. Matematicheskie voprosy chislennogo
resheniya giperbolicheskikh
sistem uravneniy [Mathematical
problems of numerical solving for hyperbolic equations systems]. PhysMatLit, 2001. (In Russian).
5. Steuer R. Mnogokriterialnaya optimizatsiya [Multiple Criteria Optimization]: Teoriya, vychisleniya i prilozheniya
[Theory, Computation, and Application]. JOHN WILEY & SONS, NY, 1992. (In Russian).
6.
Bondarev A.E. Reshenie zadachi optimizatsionnogo analiza s pomoschyu parallelnykh vychisleniy [Solving
of optimizing analysis problem by parallel computations]. Novye informatsionnye tekhnologii
v avtomatizirovannykh sistemakh: materialy pyatnadtsatogo nauchno-prakticheskogo seminara [15-th
Seminar “New Information Technologies in Automatic Systems” Proceedings],
Moscow, 2012, p.89-93. (In Russian).