Научная
визуализация как метод анализа научных данных
В. Пилюгин1, Е.
Маликова2, А. Пасько3, В. Аджиев3
1
Национальный исследовательский ядерный университет «МИФИ», Москва, Россия
2 Uformia, Фуруфлатен, Норвегия
3 Британский
национальный центр компьютерной анимации при университете Борнмута,
Борнмут, Великобритания
pilyugin@sv-journal.com, e_mal@inbox.ru, apasko@bournemouth.ac.uk, vadzhiev@bournemouth.ac.uk
Оглавление
Ряд обобщений и полученные практические результаты
Аннотация
В статье рассматривается научная визуализация
как современный компьютерный метод анализа различных научных данных при
проведении теоретических и экспериментальных исследований. Дается определение
этого метода и приводится ряд его характеристик, полученных авторами в качестве
обобщений практических результатов.
В качестве примера эффективного
инструментального средства для реализации этого метода рассматривается
программный код HyperFun. Приводятся примеры
использования HyperFun для решения задач анализа
научных данных, представляющих собой результаты компьютерного моделирования
молекулярных структур, методом визуализации. Для этих примеров подробно
рассматривается процесс решения 2-х подзадач научной визуализации, приводятся
тексты прикладных программ визуализации на языке HyperFun
и проекционные графические изображения, являющиеся результатом работы этих
программ.
Ключевые слова: научные исследования, анализ научных
данных, метод визуализации, пространственная сцена, пространственное моделирование.
Как показывает практика, под научной визуализацией, в
широком смысле, принято понимать графическое представление тех или иных научных
данных при проведении теоретических или экспериментальных исследований. Другими
словами, научная визуализация трактуется обычно как преобразование при помощи
компьютера невидимых исходных
научных данных в видимые графические
данные ( to make invisible visible
), что делается с целью последующего понимания ( анализа ) этих исходных
данных.
Мы рассматриваем научную визуализацию как современный ,компьютерный метод
анализа исходных научных данных [Nano2008] . Суть метода научной визуализации заключается в
том, что исходным анализируемым данным ставится в соответствие некоторая их
статическая или динамическая графическая интерпретация, которая визуально
анализируется, а результаты анализа этой графической интерпретации (графических
данных) истолковываются исследователем по отношению к исходным данным (см.
рис.1).
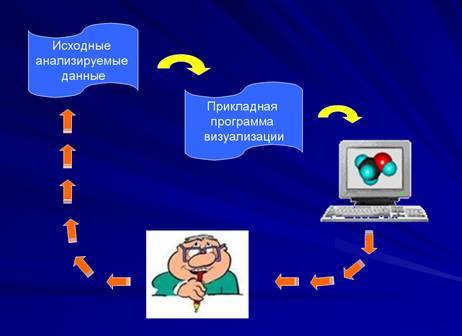
Рис. 1.
Метод научной визуализации
При такой трактовке научной визуализации как единое
целое рассматриваются собственно визуализация анализируемых научных данных (что
соответствует, как было отмечено выше, трактовке научной визуализации в широком
смысле) и визуальный анализ ее результатов. Исходные данные, анализируемые
методом научной визуализации, могут иметь различную природу. Наряду с этим,
могут различаться и цели анализа исходных данных. Соответственно, могут
различаться и используемые графические данные. Этот метод дает возможность
использовать огромные потенциальные возможности пространственно-образного
мышления исследователя в процессе анализа различных научных данных.
Развитие и усложнение этого метода, а также расширение
класса задач, для решения которых он используется, делает актуальным дальнейшую
разработку его научных и инженерных основ. В данной статье предложен ряд обобщений
практических результатов, полученных авторами при решении задач анализа
различных научных данных методом визуализации.
Ряд обобщений и полученные практические результаты
1. Прежде
всего, как нам представляется, надлежит уточнить ответ на вопрос (который на
первый взгляд кажется риторическим) - что
в контексте визуализации в общем случае следует понимать под научными данными и
анализом научных данных?
Отличительной характеристикой современных научных
исследований различных объектов той или иной природы является то, что эти исследования
осуществляются на базе все более широкого использования компьютеров. Это
справедливо как для экспериментальных, так и теоретических исследований. Когда
мы говорим о теоретических исследованиях, то имеем в виду современный стиль
таких исследований – вычислительный эксперимент, когда математическая модель
материального объекта, реально существующего или воображаемого (расчетного),
исследуется с использованием компьютера. К экспериментальным исследованиям
материальных объектов близки математические исследования различных сложных
математических абстракций с использованием компьютеров. В этом случае, подобные
математические абстракции выступают в качестве объекта исследования, т.е. здесь
имеет место своеобразный натурный эксперимент.
При проведении подобных научных исследований
получаются различные данные, описывающие исследуемый объект. Эти научные данные есть числовые данные,
отображаемые различными способами в
памяти компьютера. Они представляют собой упорядоченные конечные множества
и, как правило, сводятся к одной или нескольким связанным таблицами этих
данных, т.е. рассматриваются как числовые
табличные данные.
2. Анализу числовых табличных данных,
которые получаются либо в процессе натурного или вычислительного эксперимента,
либо в процессе исследования математической абстракции на базе компьютера, предшествует в общем случае та или иная
предварительная обработка этих данных. Целью обработки полученных «сырых»
данных является их «улучшение» в контексте дальнейшего их анализа. В качестве
типовых операций обработки данных можно выделить интерполяцию, фильтрацию и
прореживание данных. В процессе обработки эти операции могут использоваться
автономно или совместно.
В итоге
получаются новые числовые табличные данные, которые затем анализируются. В
дальнейшем будем называть эти анализируемые данные просто научными данными.
3. Процесс
анализа тех или иных научных данных можно рассматривать как решение
соответствующей задачи анализа этих
данных в следующей постановке:
Дано:
Числовые табличные данные D, описывающие исследуемый объект.
Требуется:
Получить те или иные интересующие исследователя суждения
C об исследуемом объекте.
4. Решение такой задачи анализа методом
визуализации означает сведение этой задачи к двум следующим,
последовательно решаемым задачам.
Первая
задача заключается в получении
представления анализируемых данных в виде их некоторого графического
изображения (задача визуализации исходных данных). Эта задача решается с
использованием компьютера. Вторая задача
заключается в визуальном анализе графического изображения анализируемых
данных, полученного в результате решения первой задачи. При этом результаты
анализа интерпретируются по отношению к исходным данным. Эта задача решается
непосредственно самим исследователем.
5. Aлгоритм f решения
первой задачи можно представить как
произведение (суперпозицию) следующих функциональных отображений:
f = f1 * f2 (1)
где
f1: D ![]() ( L,O )
( L,O )
f2: ( L,O ) ![]() GR
GR
D – множество исходных
числовых данных заданного вида,
L – множество геометрических
моделей воображаемых пространственных сцен (т.е. одного или нескольких
воображаемых материальных и/или абстрактных пространственных объектов) выбранного
вида,
O – множество оптических моделей этих пространственных
сцен,
GR – множество графических изображений этих
пространственных сцен выбранного вида.
Блок-схема алгоритма f представлена на рис.2.
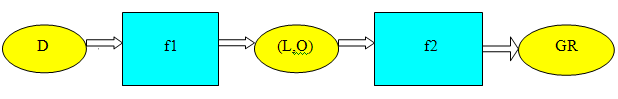
Рис.2. Блок-схема алгоритма
f
В частном случае отображение f1 может иметь вид f1: D ![]() L, а элемент
множества O при выполнении алгоритма задается исследователем.
L, а элемент
множества O при выполнении алгоритма задается исследователем.
Геометрические модели множества L представляют собой в общем случае совокупности статических
и динамических геометрических фигур с числовыми параметрами в трехмерном
евклидовом пространстве E3. Оптические модели представляют собой оптические
характеристики объектов пространственных сцен, заданные как зависимые числовые
переменные величины на множестве точек пространства E3, принадлежащих выбранной геометрической модели
сцены. В качестве таких характеристик выступают в общем случае
как коэффициенты отражения, так и преломления света, которые также могут
зависеть от времени.
Отображение f2 является параметрическим , в число параметров входят такие переменные величины как
“тип проекции”, “камеры”,”источники света”, “среда” – так называемые, атрибуты
визуализации.
Отметим, что подобные f алгоритмы
пошагового преобразования исходных данных в соответствующие графические
изображения принято, как известно, называть конвейером визуализации (visualization pipeline).
Этот термин широко используется при рассмотрении научной визуализации в
упомянутом в начале статьи широком смысле ( to make invisible visible ).
Рассмотренные
выше понятия представляют собой основу понятийного аппарата разработки
алгоритма визуализации исходных данных. Отображение f2 является классическим
отображением визуализации пространственной сцены (современной компьютерной 3D графикой), отображение f1 является отображением
пространственного моделирования исходных данных. При определении отображений f1
и f2 необходимо задавать вводимые в рассмотрение множества D, L, O, GR.
Если отображение f2 является классическим и
предполагает использование известных алгоритмов компьютерной 3D графики, то отображение f1 является менее изученным. Это отображение во многом
зависит от вида исходных анализируемых числовых данных. Так, например, эти
числовые данные могут быть как числовыми значениями количественных входных и
выходных величин исследуемой математической модели объекта, так и числовыми
значениями параметров геометрических, векторных, тензорных и других типов
входных и выходных величин этой математической модели.
Как показывает
наш опыт различных приложений научной визуализации, это отображение часто можно
представить как произведение двух отображений s1 и s2:
f1 = s1*s2 (2)
где
s1: D ![]() N
N
s2: N ![]() (
L,O )
(
L,O )
N – множество геометрических
моделей исходных данных.
В частном случае отбражения s2 может иметь вид s2: N ![]() L, а элемент
множества O при выполнении алгоритма
задается исследователем.
L, а элемент
множества O при выполнении алгоритма
задается исследователем.
В отличии от геометрических
моделей множества L, геометрические модели множества N могут представлять собой
в общем случае совокупности статических и динамических геометрических фигур с
числовыми параметрами как в трехмерном евклидовом пространстве E3,
так и многомерных геометрических пространствах. Например, в качестве такого
пространства может быть использовано многомерное евклидово пространство EN, точками которого являются n-ки
(упорядоченные совокупности из n действительных
чисел) . Само отображение s1: D ![]() N может включать
в себя в общем случае сложные геометрические построения (операции), выполняемые
как в каком-то одном, так и в нескольких геометрических пространствах.
N может включать
в себя в общем случае сложные геометрические построения (операции), выполняемые
как в каком-то одном, так и в нескольких геометрических пространствах.
Более того, используемые геометрические фигуры как в
трехмерном евклидовом пространстве E3, так и в многомерных
евклидовых пространствах EN,
могут представлять собой в общем случае полевые геометрические фигуры, то есть
множества точек с заданными на них отображениями на множества чисел, векторов
или объектов другой математической природы.
В простейшем случае множество N совпадает с множеством L, а отображение f1
приобретает вид: f1: D ![]() ( L,O ).
( L,O ).
6. Мы
рассмотрели основные характеристики решения первой задачи. Рассмотрим теперь характеристики решения второй задачи, а именно
визуального анализа графического изображения исходных данных и интерпретации
результатов этого анализа по отношению к этим данным, т.е. получения
интересующих исследователя суждений С об исследуемом
объекте. Как анализ, так и интерпретация осуществляются исследователем,
решающим задачу анализа исходных данных.
В чем заключается визуальный анализ графических
представлений исходных данных? Здесь принципиально важным является понимание того,
что визуальный анализ графического представления этих
данных по сути заключается в качественном анализе той
пространственной интерпретации, которая в рамках данного метода ставится
исходно в соответствие анализируемым научным данным в соответствии с приведенным
выше отбражением f1: D ![]() ( L,O ). Т.е.
используемые графические изображения представляют собой лишь средство
естественного и удобного для исследователя визуального анализа этой
пространственной интерпретации, с последующим истолкованием его результатов по
отношению к исходным научным данным.
( L,O ). Т.е.
используемые графические изображения представляют собой лишь средство
естественного и удобного для исследователя визуального анализа этой
пространственной интерпретации, с последующим истолкованием его результатов по
отношению к исходным научным данным.
Таким образом, метод
научной визуализации, как метод анализа научных данных, представляет собой метод пространственного моделирования этих
данных и тем самым позволяет использовать в процессе анализа разнообразных
научных данных огромные потенциальные возможности пространственно-образного
мышления исследователя.
Процесс визуального анализа графического изображения
строго не формализуем. Эффективность визуального анализа определяются опытом
исследователя, осуществляющего этот анализ изображения, и его склонностью к
пространственно-образному мышлению. Глядя
на полученное изображение, исследователь может решать 3 основные
задачи:
- анализ формы пространственных объектов,
- анализ их взаимного расположения,
- анализ графических атрибутов пространственных
объектов.
Результатом решения этих задач является формирование
исследователем соответствующих суждений о пространственной сцене. Результаты
решения этих трех задач, как было указано выше, интерпретируются исследователем
по отношению к исходным данным, т.е. в итоге им формируются соответствующие
суждения об исследуемом объекте.
Исследователь может быть либо удовлетворен
результатами анализа, либо он для получения лучших результатов повторно
выполняет алгоритм f, весь или его часть, изменяя
значения тех или иных параметров. Например, возможно получение различных
проекционных графических изображений пространственной сцены в процессе анализа
формы пространственного объекта. В результате, процесс решения задачи анализа
исходных данных методом научной визуализации усложняется и становится итеративным и интерактивным.
7. Как было отмечено
выше, метод научной визуализации,
как метод анализа научных данных, представляет собой метод пространственного моделирования этих данных. Вводимая в
рассмотрение в данном случае пространственная сцена анализируется визуально,
т.е. осуществляется чувственный анализ
этой пространственной сцены с
использованием конкретного органа чувств – человеческого глаза. Однако для
чувственного анализа пространственной сцены совместно с глазом можно использовать
также другие органы чувств – например, человеческое ухо.
Так, например, при анализе заданного скалярного поля
методом визуализации ему можно поставить в соответствие воображаемую
пространственную сцену, включающую наряду с традиционной изоповерхностью (или
несколькими изоповерхностями) также воображаемый абстрактный точечный источник
звука (его математическое описание) с амплитудой, пропорциональной величине
поля в задаваемой исследователем точке. В результате появляется дополнительная
возможность поточечного прослушивания пространственной сцены с использованием
звукового рендеринга, т.е. в этом случае имеет место расширенная научная визуализация.
8.
После того, как алгоритм f
решения 1-ой задачи определен, он
реализуется (моделируется) при помощи компьютера для заданных исходных
данных из множества D. Реализация осуществляется путем написания в соответствии
с алгоритмом f прикладной программы визуализации на
некотором входном языке программирования используемого инструментального
средства (совокупности средств) в виде некоторого программного продукта
(совокупности программных продуктов).Как было сказано
выше, алгоритм f в общем случае может быть весьма сложным. Это в свою
очередь предполагает возможность использования для его реализации развитых
инструментальных средств, позволяющих использовать в этом алгоритме весь
понятийный аппарат, вводимый в рассмотрение исследователем в рамках решения
задачи анализа научных данных методом визуализации.
Как показывает
наш опыт, в качестве такого инструментального средства хорошо зарекомендовал
себя на практике язык и программный продукт HyperFun на основе функционального представления (Function Representation, FRep) геометрических объектов. Рассмотрим
основные характеристики FRep и HyperFun.
Система понятий, используемых в HyperFun при геометрическом моделировании, включает
множества геометрических объектов (фигур), операций и отношений. FRep определяет геометрический объект в многомерном
пространстве как единое целое с помощью одной вещественной непрерывной
описывающей функции нескольких переменных в виде F(X) ³ 0 [PASS95, АПСС96]. Традиционное использование вещественных функций
охватывает: скелетоны (skeletons), генерирующие
скалярные поля или так называемые "капельные объекты" (blobby objects); примитивы
конструктивной геометрии твердых тел (
Мы рассматриваем геометрические объекты
как замкнутые подмножества Эвклидова пространства En,
определяемые описывающей функцией F(X) ³ 0, где F - непрерывная вещественная функция, и X = (x1, x2,..., xn) - задаваемая координатными переменными точка в En. Здесь неравенство F(X) > 0 задает множество
точек внутри объекта, F(X) = 0 - это изоповерхность, включающая все точки на
границе объектаб и F(X) < 0 - множество точек,
лежащих снаружи и не принадлежащие объекту. Функции могут быть определены
формулами или с помощью вычислительных процедур. Общее определение объекта
дается в многомерном пространстве, что позволяет выбирать пространство нужной
размерности в каждом конкретном случае.
В процессе моделирования может быть
определено некоторое конечное множество объектов-примитивов. Однако концептуально
это не обязательно, что позволяет иметь пустое множество объектов в
предположении, что пользователь определит их сам либо в символьном виде с
помощью формул, либо посредством вычислительных процедур. Такой подход
позволяет унифицировать очень разные виды моделей твердых тел при условии, что
удается найти функциональные представления для них или конвертировать уже
существующие объекты в желаемую форму. Таким образом, например, мы можем
совместно использовать в одной модели примитивы конструктивной геометрии,
неявно заданные объекты свободной формы, заметенные твердые тела и воксельные объекты. В работе [PASS01]]
была введена более общая модель конструктивных гиперобъемов,
которая позволяет моделировать разнородные объемные объекты в виде точечных
множеств с атрибутами такими, как материал, его плотность и другими, то есть в
виде упомянутых выше полевых геометрических фигур (см. детали в [HOMA08]).
Каждая геометрическая операция должна быть
замкнута на данном представлении, генерируя в качестве результата непрерывную
вещественную функцию. Примерами базовых операций являются
теоретико-множественные, гладкого сопряжения, офсеттинга,
биективного отображения, проецирования, декартова
произведения и метаморфозиса. Примерами отношений
являются отношения включения, принадлежности точки и пересечения.
При определении оптических моделей
пространственных объектов в HyperFun в качестве
оптических характеристик выступают коэффициенты отражения и преломления света.
Для визуализации пространственных сцен в HyperFun используются несколько программ рендеринга
с параметрами.
Моделирование на основе функционального представления
может выполнятся с помощью языка программирования высого уровня HyperFun [
HyperFun обеспечивает следующие универсальные
средства для моделирования и рендеринга:
- широкий и легко расширяемый набор
геометрических примитивов и операций;
- процедурная генерация структур
высокой сложности;
- моделирование физических свойств с
помощью точечных атрибутов;
- рендеринг
изоповерхностей при помощи их кусочно-линейной аппроксимации (полигонизации) и трассировки лучей;
- итеративное изменение параметров
модели в процессе визуального анализа.
Отображение f1, которое обсуждалось выше, в HyperFun осуществляется довольно естественно
если исходные данные представляют собой функциональные зависимости. В случае
дискретных наборов числовых данных необходимо привлечение процедур
интерполяции, позволяющих получить непрерывные описывающие функции.
Примером отображения f2, которое также обсуждалось выше, может служить
процедура кусочно-линейной аппроксимации поверхности FRep объекта набором треугольников с их
последующей проекцией на выбранную картинную плоскость. В работе [
Рассмотрим примеры решения задач
анализа научных данных методом научной визуализации.
Пример 1.
Постановка
задачи
Исследуемым объектом является расчётная молекула C2H2.
Дано
Математическая модель скалярного поля электронной
плотности этой молекулы задана в виде:
Y =f(x,y,z|t), где – x,y,z, Y заданы таблично.
Y – значение электронной
плотности
x,y,z – координаты точек пространства,
x1<x<x2
y1<y<y2
z1<z<z2
t – значение параметра, причем
функция Y задана при значениях параметра t=t1 и t=t2 (0<=t1<=1, 0<=t2<=1)
t1->Y=f1(x,y,z)
t2->Y=f2(x,y,z)
Требуется: проанализировать изменение этой функции в
зависимости от параметра t.
Будем решать эту задачу методом визуализации. В
соответствие с этим методом алгоритм
f решения
первой задачи, как описывалось выше, представляет собой суперпозицию
функциональных отображений:
f = f1 * f2
Отображение
f1 включает следующие шаги:
Определим геометрическую модель пространственной
сцены.
1) Поставим в соответствие таблично заданным функциям f1(x,y,z) и f2(x,y,z) интерполяционные функции f~1(x,y,z) и f~2(x,y,z). Введем в рассмотрение
функцию четырех переменных Y=(1-t)*f ~2+t*f~1. Геометрической интерпретацией этой функции четырех
переменных является гиперповерхность G5 в
евклидовом пространстве E5, для которой Y является
описывающей функцией. Эта геометрическая интерпретация задает отображение s1: D ![]() N, описанное
выше. Т.е. здесь
мы используем в качестве s1
суперпозицию s11 и s12, где s11 – отображение множества всевозможных
таблично заданных действительных функций f1(x,y,z) и f2(x,y,z) на
множество всевозможных соответствующих интерполяционных функций f~1(x,y,z) и f~2(x,y,z)., а s12 - известное из аналитической геометрии отображение множества
всевозможных действительных функций 4-ех действительных переменных на
множество всевозможных фигур евклидового пространства E5.
N, описанное
выше. Т.е. здесь
мы используем в качестве s1
суперпозицию s11 и s12, где s11 – отображение множества всевозможных
таблично заданных действительных функций f1(x,y,z) и f2(x,y,z) на
множество всевозможных соответствующих интерполяционных функций f~1(x,y,z) и f~2(x,y,z)., а s12 - известное из аналитической геометрии отображение множества
всевозможных действительных функций 4-ех действительных переменных на
множество всевозможных фигур евклидового пространства E5.
2) Фиксируя значение t=ti, мы можем данной гиперповерхности G5 в
пространстве E5 поставить в соответствие гиперповерхность G4 в пространстве E4 с
описанием Y= f i(x,y,z). Это
соответствует геометрической операции пересечения исходной гипероверхности
G5 гиперплоскостью с описанием t=ti с последующей проекцией результата пересечения на
пространство E4. Гиперповерхности G4 в пространстве E4 мы можем
поставить в соответствие совокупность изоповерхностей Cj в трехмерном пространстве E3 путем
выбора значений уровня cj для функции Y. Это
соответствует геометрической операции пересечения гипероверхности
G4 в пространстве E4
гиперплоскостью с описанием Y = cj с последующей проекцией результата пересечения на
пространство E3. Такая процедура задает описанное ранее отображение
s2: N ![]() L, в данном
случае, гиперповерхности G5 в
пространстве E5 на совокупность изоповерхностей Cj в пространстве E3.
L, в данном
случае, гиперповерхности G5 в
пространстве E5 на совокупность изоповерхностей Cj в пространстве E3.
3) Полученный ряд изоповерхностей будем рассматривать
как геометрическую модель воображаемой пространственной сцены, которая
определена в соответствии с исходным математическим описанием скалярного поля
электронной плотности и отображениями s1 и s2.
4) Поставим каждому из вышеупомянутых значений уровня cj для фунции Y значение цвета
изоповерхности на выбранной цветовой линейке.
Таким образом, мы полностью определили отображение f1.
Отображение
f2
Рендеринг изоповерхностей может производится
с помощью их аппроксимации треугольными сетками и их последующим графическим
представлением, либо с помощью процедуры трассировки лучей, напрямую задающей
цвет в пикселях изображения. Для простоты будем считать, что при реализации
отображения f2 значения параметров рендеринга будут выбираться по умолчанию.
Таким образом, отображение f=f1*f2 нами определено.
Решение
второй задачи:
Визуально анализируя полученные изображения на
мониторе, мы делаем суждения об изменении формы изоповерхностей при изменении
параметра t. В итоге мы делаем суждения об изменении
анализируемого скалярного поля.
Программа
на языке HyperFun,
реализующая алгоритм f1
my_model(x[3],
a[1],s[1])
{
array xt[4];
array xt2[3];
array c[1];
s[1] =
0.0;
c[1]= 0.0;
--задание
параметра t=ti;
t=0;
-- задание
координат точки в пространстве E4 {xt1,xt2,xt3,t}
xt[1]=x[1];
xt[2]=x[2];
xt[3]=x[3];
xt[4]=t;
-- задание
координат точки в пространстве E3 {xt1,xt2,xt3 }
xt2[1]=x[1];
xt2[2]=x[2];
xt2[3]=x[3];
while (t<=5) loop
-- фиксируем
значения t=ti
xt[4] = t*0.2;
-- сдвиг каждой
гиперповерхности G4 вдоль оси X
xt2[1]=x[1]+3*t;
--
интерполяционная функция табличного описания
--в файле t1->Y=f1(xt2[1],xt2[2],xt2[3])
sp1=rscalars(1,xt2,"ed1.txt");
--
интерполяционная функция табличного описания
-- в файле t2->Y=f2(xt2[1],xt2[2],xt2[3])
sp2=rscalars(2,xt2,"ed2.txt");
-- описание
спроецированного сечения гипероверхности G5 (Описывающая
функции четырех переменных Y=(1-t)*f
~2+t*f~1 ) гиперплоскостью с описанием t=ti
sp3=(1-xt[4])*sp1+xt[4]*sp2;
if (t = 0) then sp4=sp1;
else
sp4=sp4 | sp3; --
объединение всех спроецированных сечений
endif;
t=t+1;
endloop;
my_model = sp4;
}
Примечание. При построении проекционных графических изображений
для улучшения качества изображения была использована программная библиотека VTK, в состав которой входит функциональная процедура
получения описания совокупности изоповерхностей Сj в трехмерном пространстве E3 , путем
выбора значений уровня cj для заданной функции Y. Данная функциональная процедура была использована для
получения описания совокупности изоповерхностей ci, поставленных в соответствие гиперповерхности G4 в пространстве E4,
описание которой было получено с помощью приведенной выше программы на HyperFun.
Результат
работы программы

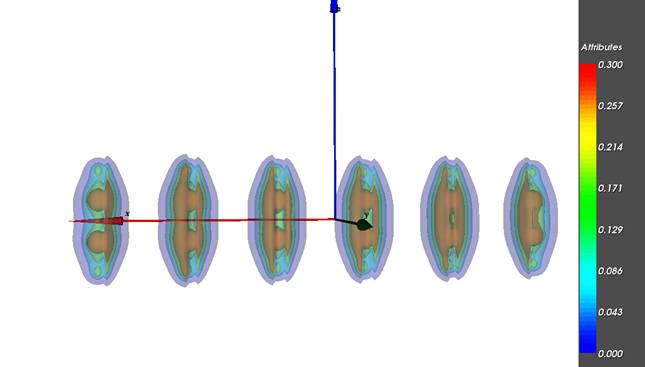
На рисунке показано результирующие проекционные
графические изображения, позволяющие осуществлять визуальный анализ
пространственной сцены и интерпретировать результаты этого анализа по отношению
к исходным данным, т.е. формировать интересующие исследователя суждения о
рассматриваемом объекте.
Рассмотрим проекционное графическое
изображение полученного ряда
изоповерхностей. Анализируя ряд изоповерхностей
пользователь делает суждения о характере изменения формы поля электронной
плотности на заданном временном промежутке 0<=t<=1. Анализируя форму каждой
совокупности изоповерхностей, а также цветовое покрытие каждой изоповерхности
для определенного ti, исследователь делает суждение о
скалярном поле электронной плотности в момент ti. На рисунках ниже представлены
проекционные графические изображения рассматриваемого ряда изоповерхностей при
задании различных значений параметров рендеринга –
положение камеры.
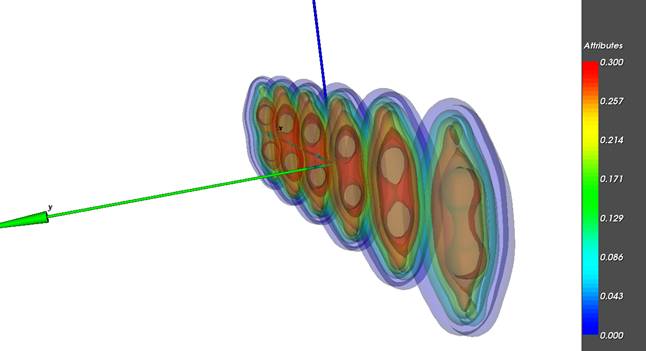
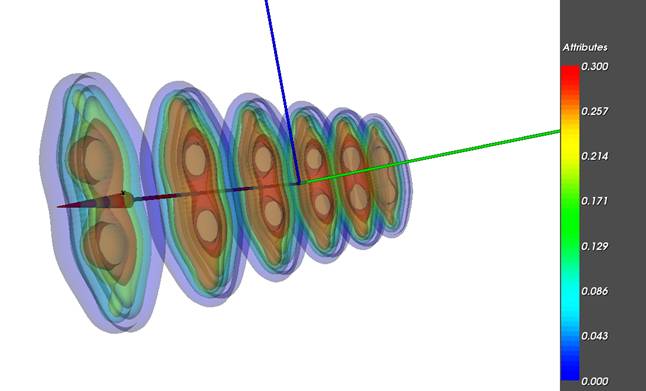
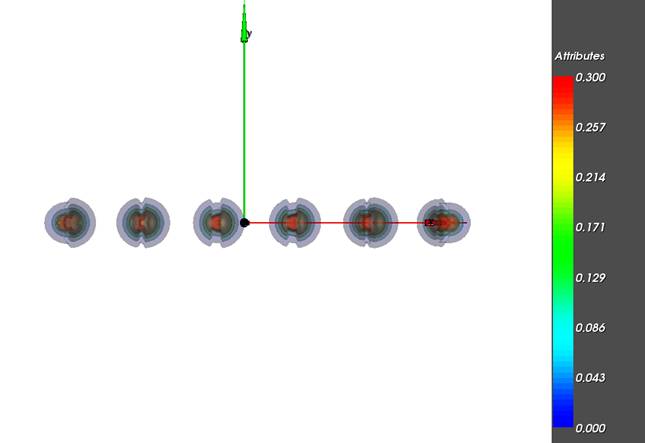
Пример 2.
Постановка
задачи
Исследуемым объектом является скалярное поле
электронной плотности и поле электростатического потенциала для расчётной
молекулы NCH.
Дано
Математическая модель скалярного поля электронной
плотности этой молекулы задана в виде:
Y =f(x,y,z), где
x,y,z, Y заданы
таблично.
Y – значение электронной
плотности
x,y,z – координаты точек пространства,
x1<x<x2
y1<y<y2
z1<z<z2
и математическая модель поля электростатического
потенциала задана в виде:
U=q(x,y,z), где –
x,y,z, U заданы
таблично.
U – значение
электростатический потенциал
x,y,z – координаты точек пространства,
x1<x<x2
y1<y<y2
z1<z<z2
Требуется проанализировать эти два поля (построить совместные
суждения о них)
Будем решать эту задачу методом визуализации. В
соответствие с этим методом алгоритм
f решения
первой задачи представляет собой
суперпозицию функциональных отображений:
f = f1 * f2
Отображение
f1 включает следующие шаги:
Определим геометрическую модель пространственной
сцены.
1) Аналогично Примеру 1, поставим в соответствие
функции f совокупность изоповерхностей Сj, соответствующих определенным значениям Y.
2) В данном случае изоповерхность является полевой
геометрической фигурой, на которой задано отображение на множество
действительных чисел q(x,y,z).
Определим оптическую модель пространственной сцены.
3) Значение функции q(x,y,z) для точек (х,y,z) каждой из изоповерхностей Cj будем рассматривать как значение цвета в данных
точках.
Отображение
f2
Рендеринг можно задать одним из способов, описанных в Примере
1, однако для каждой точки изоповерхности будем использовать значение цвета присвоенное в соответствии с выбранной выше оптической
моделью.
Таким образом, отображение f=f1*f2 нами определено.
Решение
второй задачи:
Визуально анализируя полученные изображения на
мониторе, мы анализируем форму и цветовое покрытие изоповерхностей и делаем
суждения об исходных полях.
Программа
на языке HyperFun,
реализующая алгоритм f1
my_model(x[3],
a[1],s[1])
{
array c[1];
c[1] =
0.0;
s[1]=0.0;
-- описание
полевой геометрической фигуры, поставленной в соответствие полю электростатического
потенциала
a1=rscalars(1,x,"ed11.txt");
-- описание
поля электростатического потенциала
t=rscalars(2,x,"p11.txt");
c[1]=t;
model=a1-0.02;
tmp = hfA_SetAttributes(model,s,c);
my_model =model;
}
Примечание. Как и в примере 1, при построении проекционных
графических изображений для улучшения качества изображения была использована
программная библиотека VTK, в состав
которой входит функциональная процедура получения описания совокупности
изоповерхностей Сj
в трехмерном пространстве E3 , путем выбора значений уровня cj для заданной функции Y.
Результат
работы программы
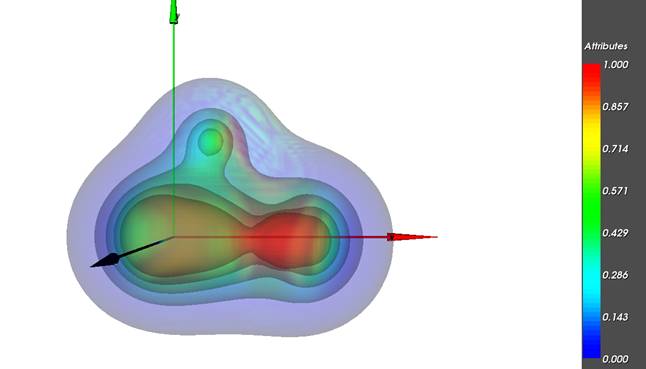
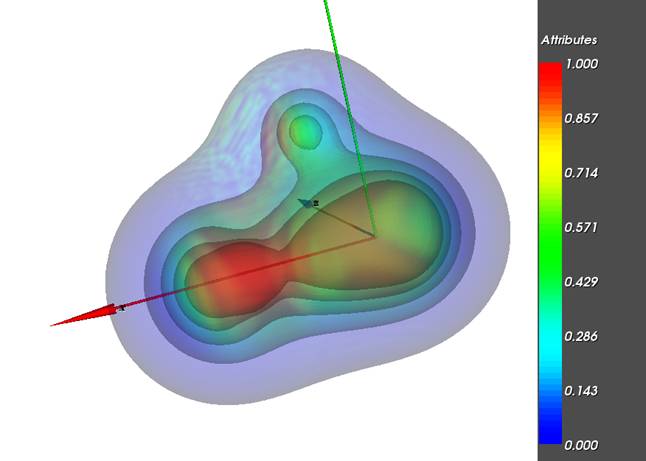
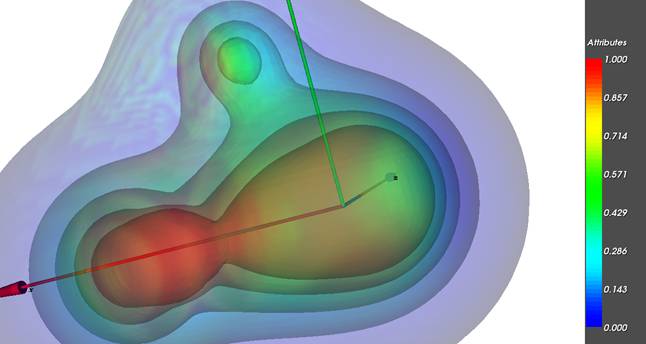
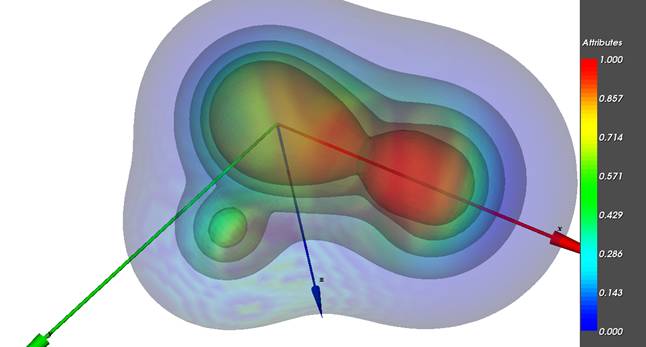
На рисунках показаны результирующие проекционные
графические изображения, позволяющие, как и в первом примере, осуществлять
визуальный анализ пространственной сцены и интерпретировать результаты этого
анализа по отношению к исходным данным, т.е. формировать интересующие
исследователя суждения о рассматриваемом объекте. Анализируя форму совокупности
изоповерхностей исследователь может делать суждения о
скалярном поле электронной плотности, анализируя совместно цветовую раскраску и
форму этих изоповерхностей пользователь делает суждения о поле
электростатического потенциала и поле электронной плотности, т.е. осуществляет
одновременный анализ 2-х скалярных полей.
Таким образом, мы рассмотрели ряд теоретических
обобщений полученных нами практических результатов при решении задач анализа
различных научных данных методом научной визуализации.
Хотелось бы отметить, что с нашей точки зрения
введение отображений s1 и s2 является принципиальным, несмотря на то, что во
многих рассматриваемых в наше время задачах анализа данных они являются
тривиальными. С усложнением видов данных и с повышением их размерности важность
строгого задания отображений данных на геометрические модели будет
безусловно возрастать. В противном случае решение второй задачи, а именно
визуального анализа графического изображения исходных данных и интерпретации
результатов этого анализа по отношению к этим данным, будет сильно затруднена.
Как нам представляется, сформулированные обобщения
могут быть полезны читателям.
Следует отметить, что авторами продолжаются работы в
данном направлении.
[Nano2008] Пасько А.А., Пилюгин В.В. Научная визуализация и
ее применение в исследованиях наноструктур // Rusnanotech. Международный форум по нанотехнологиям.
Сборник тезисов докладов научно-технических секций 2008. Москва. С. 189.
[PASS95]
Pasko A., Adzhiev V., Sourin A., Savchenko V., Function
representation in geometric modeling: concepts,
implementation and applications, The Visual Computer, vol.11, No.8, 1995,
pp.429-446.
[АПСС96]
Аджиев В.Д., Пасько А.А., Савченко В.В., Сурин А.И.,
Геометрическое моделирование с использованием действительных функций.-Открытые системы. - 1996,
№5(19)б с. 14-18.
[PASS01] Pasko A., Adzhiev V., Schmitt B.,
Schlick C., Constructive hypervolume
modeling, Graphical Models, vol. 63, No. 6, 2001, pp.
413-442.
[HOMA08] Heterogeneous
Objects Modelling and Applications, Lecture Notes in Computer Science, vol.
4889, Eds. Pasko A., Adzhiev
V., Comninos P., Springer Berlin / Heidelberg, 2008,
285 p.
[
[
Scientific
visualization as method of scientific data analysis
V.
Pilyugin1, E. Malikova2, A. Pasko3, V. Adzhiev3
1 The National
Research Nuclear University "MEPhI",
Moscow, Russia
2 Uformia, Furuflaten, Norway
3 The National
Centre for Computer Animation, Bournemouth University, Poole, UK
pilyugin@sv-journal.com,
e_mal@inbox.ru, apasko@bournemouth.ac.uk, vadzhiev@bournemouth.ac.uk
Abstract
The modern computer
method of scientific data analyses that is widely used at theoretical and experimental
research - scientific visualization method is considered. The definition of
this method and its main characteristics, that are generalizations made by
authors as the results of practical experience, are given.
The HyperFun language is considered as an example of an
effective tool for this method implementation. Examples of using HyperFun for solving problems of analysis of scientific
data that are the results of molecular structures computer modeling are given.
For these examples, the 2 sub problems of scientific visualization solving is considered , the texts of the scientific visualization
programs and graphics that are the result of these programs are given.
Keywords: scientific research, scientific visualization method,
scientific data analyses, Hyperfun, computer scene,
3d modeling.
References
[Nano2008] Pasko A., Pilyugin V., Scientific
visualization and it’s
application at nanostructures research. Rusnanotech. International natechnology forum theses 2008.
Moscow. С. 189.
[PASS95] Pasko A., Adzhiev V., Sourin A., Savchenko V., Function
representation in geometric modeling: concepts, implementation and
applications. The
Visual Computer, vol.11, No.8, 1995, pp.429-446.
[АПСС96] Adzhiev V., Pasko A., Savchenko V., Sourin A., modelling
with real –valued functions. Open systems. - 1996, №5(19)б
с. 14-18.
[PASS01] Pasko A., Adzhiev V., Schmitt B., Schlick
C., Constructive hypervolume modeling. Graphical Models, vol. 63, No. 6, 2001,
pp. 413-442.
[HOMA08] Heterogeneous
Objects Modelling and Applications, Lecture Notes in
Computer Science, vol. 4889, Eds. Pasko A., Adzhiev V., Comninos P., Springer
Berlin. Heidelberg,
2008, 285 p.
[ACF*99] Adzhiev V., Cartwright R., Fausett
E., Ossipov A., Pasko A., Savchenko V., HyperFun project: a
framework for collaborative multidimensional F-rep modeling. Implicit Surfaces '99, Eurographics/ACM
SIGGRAPH Workshop, J. Hughes and C. Schlick (Eds.),
1999, pp. 59-69. Available at: http://www.hyperfun.org
[PPP86] Pasko А.А., Pilyugin V.V., Pokrovsky V.N., Geometric modelling
in tasks of function of three variable analyses: Report OIYI Р10-86-310, Dubna, 1986. (in Russian)
Publication in English: Computers and
Graphics, vol.12, # 3/4, 1988, pp. 457-465.