Статья посвящена разрабатываемой авторами системе научной визуализации. Под научной визуализацией понимается методика перевода абстрактных объектов в геометрические образы, что дает возможность исследователю наблюдать результаты численного моделирования. Таким образом, в цепочке визуализации находятся вычислительная программа, генерирующая числовые данные, процедура построения геометрического объекта на основе этих данных и среда, позволяющая проводить манипуляции со сценой, куда помещены построенные объекты. Основным отличительным свойством разрабатываемой системы является поддержка любых форматов исходных данных и видов отображений. Это достигается за счет богатого встроенного программного интерфейса управления визуальными объектами, источниками света, камерами, историей работы и др. Предполагается, что для каждой новой задачи визуализации программируется индивидуальный вид отображения, отвечающий задаче и запросам исследователя. Система реализована на языке C# для среды исполнения .NET 4.0 для операционных систем Microsoft Windows. В настоящее время предусмотрено подключение пользовательских процедур, оформленных в виде DLL-библиотек для среды .NET, в виде скриптов на языке Ruby и в виде консольного приложения, выдающего команды в выходной поток. Приводятся примеры задач, для исследования которых в настоящее время применяется разработанная система.

Ключевые слова: научная визуализация, система визуализации, подключаемые внешние модули.

1. Введение.

В основе процесса научной визуализации лежит методика перевода абстрактных объектов в геометрические образы, что дает возможность исследователю наблюдать результаты численного моделирования явлений (см. рис. 1).

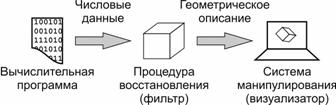
image description

Рис. 1. Схема процесса визуализации

Средства научной визуализации разделяются на три класса:

1. Универсальные системы, которые включают широкий набор алгоритмов построения различных типовых представлений. Например, это известные системы ParaView и AVS.

2. Универсально-специализированные системы, ориентированные на визуализацию объектов определенного типа. Например, это такие пакеты как IVS3D (геоинформация), VENUS (молекулярные структуры), VolVis (разреженные трехмерные массивы).

3. Специализированные системы, созданные специально для данного исследовательского проекта или даже конкретного пользователя.

Системы первых двух классов хороши тем, что позволяют в подходящих случаях быстро получить результат. Однако им присущи и принципиальные недостатки. Вложенные в такие системы виды отображения не всегда удовлетворяют всем требованиям пользователей. Добавление собственных видов отображения иногда невозможно, а иногда сопряжено с большими трудностями. Кроме того, универсальные системы, как правило, сложны в освоении.

Идеальный вариант для любого пользователя – система третьего типа, то есть, созданная специально под его задачу с учётом всех его запросов и пожеланий. Проблема заключается в том, что создание подобных систем требует значительных затрат и каждый раз ведется практически «с нуля».

Замечено, что при визуализации той или иной сущности специфическими являются выбор конкретного двух- или трехмерного геометрического представления абстрактного объекта (вида отображения) и разработка алгоритма построения этого представления на основе данных, производимых вычислительной программой. С другой стороны, инструментарий манипулирования полученными геометрическими объектами (перемещение, повороты и т.п.), как правило, совпадает для различных задач.

Таким образом, появляется идея о выделении повторяющихся компонент на инфраструктурный уровень. Удачная реализация этого уровня позволит существенно сократить объем предпринимаемых усилий при разработке новых специализированных систем научной визуализации.

В настоящей работе описывается разрабатываемая авторами среда визуализации (см. рис. 2), которая реализует представленную идею. Среда предоставляет весьма богатый пользовательский интерфейс, позволяющий удобно манипулировать имеющейся сценой, а также включает мощное ядро, дающее возможность хранить трёхмерную сцену и динамически работать с ней посредством программного интерфейса (API). При этом процедуры восстановления геометрических представлений выносятся во внешние программные модули (плагины), что позволяет настраивать систему под конкретные нужды.

Таким образом, среда играет роль «конструктора», позволяющего создать новые специализированные под конкретные задачи системы визуализации.

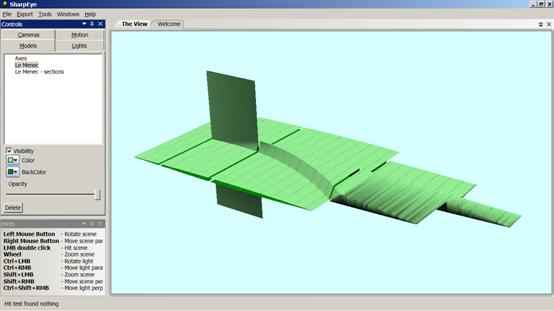
Рис. 2. Снимок экрана главного окна программы визуализации.

Необходимо отметить, что источником предложенных идей и решений является опыт создания систем визуализации, накопленный в ИММ УрО РАН (Екатеринбург, Россия) в течение более 20 лет. Одним из главных направлений, обозначившим необходимость программного обобщения компонент специализированных систем визуализации, послужили работы, связанные с задачами оптимального управления и дифференциальных игр (см. например [1-4]). Некоторые решения, представленные в настоящей работе, опробовались в начале 2000-ых годов при реализации прототипа системы визуализации [5].

2. Структура системы.

Текущая версия конструктора систем визуализации написана на языке C# для среды исполнения Microsoft .NET 4.0. При разработке использована оконная библиотека WPF и библиотека трёхмерной графики Media3D.

Для разработки была выбрана следующая схема системы (см. рис. 3).

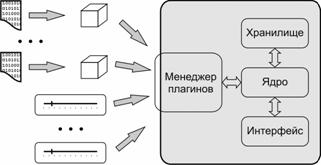
image description

Рис. 3. Схема разрабатываемой системы; слева показаны
два типа модулей – модули-фильтры и модули с реализацией
нестандартных элементов пользовательского интерфейса

Ядро является связующим элементом системы, инициализирует остальные элементы при запуске программы и обеспечивает обмен информацией между компонентами в процессе работы.

Отдельные компоненты системы реализуют те или иные интерфейсы (в смысле языка C#). Вызов тех или иных процедур компонента осуществляется вызовом соответствующих методов соответствующего интерфейса.

2.1. Хранилище.

В хранилище размещаются все данные по объектам, используемым при визуализации: источники света, камеры, модели с их иерархией. Кроме того, хранилище дает возможность содержать и невизуальные данные.

При создании объекта в хранилище ему присваивается (пользователем или модулем) уникальное внутреннее имя.

Классы визуальных объектов – моделей, камер и источников света – содержат в себе экземпляры соответствующих классов из библиотеки Media3D (Model3D, ProjectionCamera и Light). Кроме того, они хранят и общие стандартные свойства: внутреннее имя, отображаемое описание и булевский флаг, трактуемый для моделей как видимость, для камер как активность, для источников света как включенность.

У объектов-источников света дублируются свойства цвета и яркости класса из библиотеки Media3D. Это сделано для того, чтобы их можно было связать с соответствующими элементами управления в рамках интерфейсной части программы.

У объектов-камер главным запоминаемым свойством является матрица преобразований, определяющая точку зрения данной камеры. Эта матрица изменяется, когда пользователь манипулирует сценой при выбранной данной камере и накладывается на сцену, когда происходит переключение к этой камере с другой. Кроме того, в объекте камеры хранятся флаги, указывающие какие манипуляции сценой разрешены, а какие нет (перемещения в разных плоскостях/вращение/масштабирование), когда данная камера активирована. Это сделано, в частности, для того, чтобы имелись три камеры с фиксированным направлением зрения (вдоль координатных осей), так как некоторые преобразования (например, перемещения источников света) неудобно делать при произвольной точке зрения, которую может предоставлять камера, в которой подбирается нужная картинка визуализируемого объекта. Кроме того, каждая камера может быть сделана как перспективной, так и ортогональной.

Главным типом объектов, с точки зрения пользователя, является модель. Модель – это объект трехмерной сцены, являющийся визуальной сущностью. В Media3D существует единственный тип объекта – поверхность. Поэтому базовыми операциями с моделью является ее создание и наполнение треугольниками, составляющими соответствующую поверхность. Заполнение треугольниками ведется в два этапа. На первом создается набор точек, которые будут вершинами тех или иных треугольников. При добавлении точки возвращается ее индекс в массиве вершин данной модели. На втором этапе добавляются треугольники как тройки индексов точек. При этом лицевой стороной треугольника считается та, на которой его вершины обходятся против часовой стрелки относительно взгляда c нормали к этой стороне. После окончания добавления треугольников модель помещается в сцену. При этом библиотекой Media3D вычисляются аппроксимирующие внешние нормали в каждой точке. Они находятся как среднее арифметическое внешних нормалей всех треугольников, имеющих данную точку своей вершиной, и используются в алгоритмах сглаживания поверхности. Отсюда важным моментом при создании поверхности является правильный выбор узловых точек. В тех местах, которые должны быть сглажены, узлы должны быть общие для всех треугольников, в них сходящихся. Для мест, где явно должна быть негладкость поверхности, узлы нужно дублировать для каждого куска гладкости.

Кроме того, каждая модель обладает набором свойств. С одной стороны, работа со свойствами требует некоторой унификации; с другой – сами свойства могут быть весьма разнообразными по своим типам, назначению и методам работы. Поэтому хранятся свойства в ассоциативном массив (словаре) парами имя–значение; «значение» есть величина типа Object и позволяет помещать на хранение сущности любого типа. При этом пользователю нужно после получения значения из хранилища явно приводить его к нужному типу. Для осуществления той или иной автоматизации, основанной на связывании (binding) в среде определены классы аксессоров – объектов, имеющих типизированное поле, участвующее в связывании, и «знающих» как переработать получаемую величину в значение поля; прописываются пользователем самостоятельно при использовании нестандартных свойств.

С каждым свойством можно связать элемент пользовательского интерфейса, который будет появляться в области управления объектом при его выборе и отображать текущее значение данного свойства. Через этот элемент управления можно менять значение. На этом механизме реализованы, в том числе, и стандартные свойства объекта: прозрачность, цвета и другие.

Для организации структуры используется понятие объекта-группы. В начале работы программы существует единственная корневая группа. Затем при необходимости создаются другие группы и объекты сцены. Каждая группа может быть назначена дочерней для какой-то существующей группы, а каждый объект должен быть помещен при создании в одну или несколько существующих групп (по умолчанию – в корневую группу). Например, если загружаются данные нескольких примеров, в рамках каждого из которых существует несколько типов данных. Тогда, с одной стороны разумно каждый объект размещаться в группу того примера, которому он соответствует, а кроме того, в группу объектов соответствующего типа (для возможности одновременной работы со свойствами всех объектов одного типа). В настоящей версии программы при выборе группы пользователь имеет возможность изменять параметры, присущие всем объектам, хранящимся в поддереве групп выбранной группы.

Невизуальные данные позволяют помещать в хранилище произвольные двоичные данные, например, результаты промежуточной обработки входных данных. Невизуальные данные могут быть сохранены на диске и быть доступными во время других сессий работы с системой. При запросе невизуальных данных из хранилища система проверят наличие соответствующих данных в памяти; при отсутствии проверяется дисковое хранилище и при возможности соответствующий объект восстанавливается оттуда, и только в случае полного отсутствия соответствующего объекта об этом извещается вызывающая процедура.

2.2. Менеджер модулей.

При запуске системы менеджер внешних модулей производит поиск модулей (сборки EXE- и DLL-, а также скриптовые файлы), находящихся в каталоге программы и имеющих заранее оговоренную структуру.

В настоящее время имеется два типа внешних модулей: реализующие фильтры, то есть, процедуры перевода числовых данных в геометрические объекты, и реализующие функционал нестандартных элементов пользовательского интерфейса. Первые файлы должны реализовывать интерфейс IFilter, вторые – интерфейс IUIControl. Классы интерфейсов предоставляются в библиотеке, поставляемой с системой.

После того, как все такие сборки выявлены, они загружаются в память, производится их инициализация (вызов соответствующих методов интерфейса) и учет во внутренних структурах менеджера.

2.3. Интерфейс пользователя.

При открытии программы пользователь попадает на вкладку стартовой страницы (см. рис. 4).

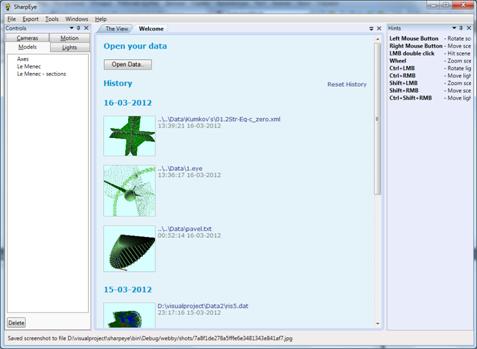
Рис. 4. Снимок экрана начальной вкладки программы.

Эта вкладка содержит кнопку для загрузки данных (она дублирует соответствующий пункт меню) и историю загрузок. Каждый пункт истории загрузок включает путь к соответствующему файлу, время загрузки и снимок экрана после загрузки этого файла.

Основная вкладка при работе программы – The View – предназначена для отображения сцены и манипулирования ею (см. рис. 5). Она автоматически открывается после загрузки данных.

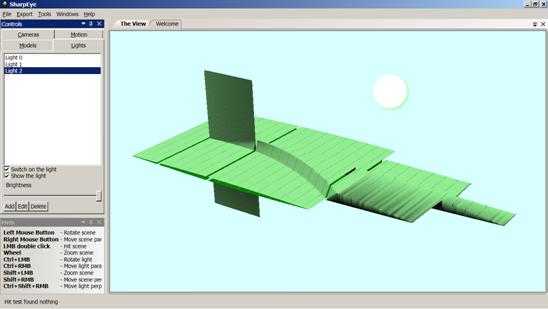
Рис. 5. Основная вкладка программы. Показано подсвечивание
текущего выбранного источника света (шар выше основного объекта).

Манипуляция сценой производятся при помощи движений мыши с зажатыми левой или правой ее кнопками, а также теми или иными клавишами на клавиатуре (Shift/Ctrl/Alt). Конкретные действия закрепляются за теми или иными сочетаниями клавиш в файле конфигурации программы.

Отображения вспомогательной информации вынесено на дополнительные панели (слева на рис.5). В настоящее время реализовано две дополнительные панели: панель управления системой (на рис. 5 слева вверху) и панель подсказок по управляющим вкладками (на рис. 5 слева внизу).

На панели управления системой имеется несколько вкладок, каждая из которых отображает и позволяет выбирать объекты различных классов и управлять ими.

Вкладка Lights: отображается список источников света, кнопки для добавления новых источников света, редактирования свойств текущего выбранного источника и для удаления текущего выбранного источника света. Когда в списке выбран тот или иной источник света, он прорисовывается в сцене в виде шара, расположенного в соответствующей точке пространства (см. рис. 5).

Вкладка Cameras: отображается список камер, кнопки для добавления новой камеры, редактирования свойств и удаления текущей выбранной камеры, а также восстановления исходной точки зрения выбранной камеры. Все манипуляции с точкой зрения привязываются к текущей выбранной камере. При выборе другой камеры происходит переключение на нее, что приводит к изменению точки зрения. При манипуляции точкой зрения одной камеры другие камеры сохраняют свою точку зрения. В настоящее время при запуске системы добавляются три камеры для проекций (их запрещено вращать) и одна камера полной функциональности – для работы в 3D. Камеры проекций удобны для точного позиционирования света.

Вкладка ModelTree: отображается иерархия моделей. При выборе объекта отображаются все элементы управления, которые при создании объекта были ассоциированы с теми или иными его свойствами. Любой объект по умолчанию обладает свойствами цвета лицевой и изнаночной поверхностей, прозрачности (от 0 – полностью прозрачный – до 1 – полностью непрозрачный) и видимости/невидимости. При выборе группы отображаются элементы управления, общие для всех объектов, содержащихся в этой группе и в ее дочерних.

После того, как желаемое изображение получено, его можно экспортировать вовне программы для дальнейшего использования (например, вставки в статью). Изображение можно экспортировать в буфер обмена, в файл растрового графического формата, либо в Интернет на специальный сервер. Трехмерную сцену можно экспортировать в файлы разных форматов, которые могут быть прочитаны другими системами и также в Интернет, откуда они могут быть просмотрены удаленно при помощи WebGL в браузере.

На видеозаписи 1 показан сеанс работы пользователя в системе.

Видео 1. Сеанс работы в системе: http://youtu.be/hyyCmq_t-Q0.

3. Программное управление системой.

Система подразумевает обширные возможности по программному управлению. Практически весь представленный в ней функционал доступен к использованию из внешних модулей.

Основу такого доступа составляют .NET интерфейсы, описанные далее в разделе «3.1. Программный интерфейс системы». Также доступ возможен и с помощью других механизмов (см. ниже раздел 3.4).

По сути, система является платформой, возможности которой можно расширять, использовать и адаптировать для конкретных задач визуализации.

3.1. Программный интерфейс системы.

Программный интерфейс системы соответствует описанию, данному ранее в разделе «2. Структура системы». Вкратце повторим это описание.

Система содержит в себе сцену (хранилище). Сцена содержит в себе модели, камеры, и источники света. Модель – это визуальный объект, который содержит в себе набор треугольников для отображения и дополнительные атрибуты, такие как цвет модели, прозрачность модели и т.д. Модели можно объединять в группы, причем каждая модель может состоять одновременно в нескольких группах.

Все обозначенные выше сущности поддаются внешнему программному управлению. Рассмотрим кратко предлагаемый программный интерфейс.

Базовые методы сцены (интерфейс IStorage):

AddModel (string name) – создает в сцене новую модель с именем name. Если данное имя занято уже существующей моделью, то последняя стирается.

GetModelByName (string name) – возвращает ссылку на модель с данным именем.

Базовые методы моделей (интерфейс IModel3D):

AddNode(double x, double y, double z) – добавляет вершину в модель. Возвращает номер добавленной вершины.

AddTriangle(int A, int B, int C) – добавляет треугольник в модель. Параметры A,B,C указывают номера вершин, формирующих треугольник.

Пример использования базовых методов системы представлен на рис. 6.

var model = storage.AddModel("sample1");

var i = model.AddNode(0,2,2);
model.AddNode(3,5,0);
model.AddNode(2,2,7);
model.AddTriangle(i,i+1,i+2);

Рис. 6. Пример использования API системы.

Кроме представленных методов, в системе существует целый ряд дополнительных методов. Например, для моделей это методы:

· Управления базовыми свойствами отображения, такими как цвет лицевой и обратной стороны треугольников, прозрачность, и др.

· Более тонкого добавления треугольников с автоматической переориентации для правильного отображения лицевых и обратных сторон формируемых поверхностей.

· Добавления в модели сфер, параллелепипедов, конусов и других примитивов.

· Указания дополнительных параметров моделей, графических элементов управления этими параметрами и кода, реагирующего на их изменения.

· Указания палитры для раскраски модели.

· Обратной связи при кликах по треугольникам модели.

Более подробно программный интерфейс моделей, а также и всей системы в целом, описан в поставляемой документации.

3.2. Создание фильтров на языке C#.

Основные модули системы – так называемые фильтры. Каждый фильтр отвечает за загрузку данных определенного формата. При загрузке система находит фильтры в рабочем каталоге и в дальнейшем использует их для загрузки пользовательских данных.

Интерфейс фильтров IFilter задает три метода:

public void Start (IStorage s);

public double Feel (string filepath, Probe p);

public bool Load (string filepath, IStorage s);

Метод Start, реализуемый в фильтре, обеспечивает его инициализацию и вызывается менеджером плагинов при запуске системы. В него передается ссылка на объект-хранилище (IStorage s).

Метод Feel используется менеджером модулей, чтобы определить, какой из фильтров применить для чтения того или иного файла данных. При команде на загрузку файла менеджер модулей поочередно вызывает этот метод у всех фильтров, передавая туда имя читаемого файла (string filepath) и некоторую дополнительную информацию о файле в структуре Probe. В частности, передается некоторая начальная порция данных читаемого файла. Метод Feel должен вернуть вещественное число от 0 до 1 – свою «уверенность» в том, что данный файл должен обрабатываться именно этим фильтром. В итоге файл считывается тем фильтром, который выдал наибольшую «уверенность».

Наконец, метод Load вызывается для чтения данного файла, имя которого передается в параметре filepath. Для создания модели используется ссылка IStorage на сцену, которая содержит соответствующие методы (см. 3.1).

Таким образом, для того, чтобы написать собственный фильтр, нужно создать проект .NET-библиотеки, включить в его состав библиотеку, поставляемую вместе с системой и описывающую .NET-интерфейсы системы, создать собственный класс, унаследовав его от IFilter, и реализовать указанные методы. Полученную библиотеку следует поместить в подпапку Plugins папки пакета, после чего данный фильтр может использоваться системой.

3.3. Создание фильтров на языке Ruby.

Применяя систему на практике, авторы обнаружили, что далеко не для всех задач визуализации необходима мощь языка C#. Оказалось, что многие задачи можно весьма лаконично решать с помощью скриптовых языков.

Одним из ярких представителей этого семейства языков является Ruby. Чтобы создать модуль для системы визуализации на Ruby, достаточно создать файл с расширением «.rb» и разместить его в каталоге «Scripting». При запуске система исполняет найденные скрипты с помощью интерпретатора IronRuby.

Система считает модуль фильтром (загрузчиком данных), если в нем обнаруживаются глобальные методы feel и load. Семантика этих методов, а также логика работы с скриптовыми фильтрами, аналогичны описанию, изложенному выше для создания фильтров на языке C#.

Далее в разделе 4.1. будет приведен пример фильтра на языке Ruby.

3.4. Расширенные возможности по управлению системой.

С целью повышения удобства использования системы, авторами прорабатывается ряд дополнительных способов управления ею.

· Создание модулей на языке Pascal. Проведены эксперименты по созданию DLL-сборок фильтров в среде Pascal ABC.NET.

· Прямое управление системой из другой .NET-программы. Система может быть запущена в качестве .NET-сборки, например, из консольного приложения, или встроена в оконное приложение.

· Взаимодействие на основе COM. Возможность проработана для нестрогих интерфейсов IDispatch и опробована для языка JavaScript.

· Загрузка сцены в командном формате. Поставлен эксперимент, в котором текстовый файл считывается и интерпретируется в синтаксисе Ruby. При этом файл может содержать как просто данные, так и управляющие конструкции (обозначенные особо). Данный эксперимент может быть расширен введением двоичных форматов данных.

· Управление системой из произвольных программ с помощью стандартных потоков. Поставленный эксперимент с интерпретацией файлов позволил реализовать особый вид фильтров – загрузку данных с помощью внешних консольных программ. Для реализации запроса feel внешняя программа запускается с ключем –f, и от нее ожидается вывод результата от 0 до 1 на поток stdout. В режиме load от программы ожидаются команды на stdout, аналогичные файловым.

Разумеется, данные направления не исчерпывают всех возможностей по развитию взаимодействия с системой. Поиск и реализация новых направлений осуществляются в связи с нарастающей практической необходимостью.

4. Примеры использования системы.

4.1. Задача исследования решения задачи Дирихле.

В Отделе динамических систем Института Математики и Механики УрО РАН изучается задача [6] быстродействия с круговой вектограммой скоростей на плоскости и связанная с ней задача Дирихле для дифференциального уравнения Айзекса – Беллмана. Основным компонентом решения является функция u(x, y) евклидова расстояния до целевого множества. Её линии уровня (волновые фронты) строятся с помощью предложенного А.А.Успенским конечно-разностного оператора. При этом получаемая сетка является нерегулярной.

Был разработан специальный модуль для системы визуализации, который позволяет добавлять в сцену получающуюся сетку и график функции u(x, y), визуально исследовать локальные свойства этой функции (гладкость, дифференцируемость по направлениям) и глобальные свойства (выпуклость, вогнутость).

Пример построения функции расстояния до множества M – подграфика функции y = x⁴представлен на рис. 7.

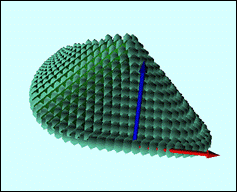
Рис. 7. Графики функции расстояния до различных множеств.

Рассмотрим вопрос создания модуля визуализации для этой задачи более подробно. Исходные данные представляют собой набор точек, аппроксимирующих рассчитанную поверхность. Эта поверхность расположена над плоскостью XY и однозначно проецируется на нее. Задача визуализации – показать данные точки и поверхность, формируемую ими.

Исходные данные содержатся в формате, представленном на рис. 8.

X Y Z

-3.4000 11.5600 0

-3.2000 10.2400 1.5

-3.0000 9.0000 2

…..

Рис. 8. Формат данных для задачи 4.1.

Первая строка всегда содержит упоминание переменных X,Y,Z. В каждой из последующих строк содержится координата очередной точки.

Код фильтра на языке Ruby, реализующий данный алгоритм, представлен на рис. 9. Модуль формирует две модели – для отображения точек и для отображения поверхности. Проводится загрузка точек и для каждой точки в первую модель добавляется сфера, обозначающая точку. Далее проводится триангуляция с помощью алгоритма Делоне, и результат – набор треугольников – отправляется во вторую модель.

# Фильтр .\Scripting\Lebedev\Surface1.rb

require 'Triangulator'

def feel(p) # Файл данных выявляем по наличию «X Y Z» в первой строке

p.first_lines =~ /X\s+Y\s+Z/ ? 1.0 : 0.0

end

def load(p)

m = scene.add_model( "#{p.name} points" )

file = File.new( p.path , "r")

file.gets # пропустим первую строку

vertices = List.of(Triangulator::Geometry::Point).new

while line = file.gets

items = line.strip.split(/\s+/) [0..2] # выделим 3 числа

next if items.length == 0

x,y,z = items.map{ |i| i.to_f }

m.add_sphere( x, y, z, 0.10, 3, 2 )

vertices << Triangulator::Geometry::Point.new(x,y,z)

end

puts "Triangulating #{vertices.count} nodes"

tris = Triangulator::Delauney::Triangulate(vertices)

puts "We got #{tris.count} triangles"

m2 = scene.add_model( "#{p.name} surface" )

vertices.each{ |v| m2.add_node( v.X, v.Y, v.Z ) }

tris.each{ |t| m2.add_triangle( t.p2, t.p1, t.p3 ) }

puts "Well done"

end

Рис. 9. Код модуля визуализации задачи 4.1.

Принципиальным в показанном примере является малый объем кода, потребовавшийся для решения задачи.

4.2. Задача исследования максимальных стабильных мостов.

Как отмечено во введении, задачей, в значительной степени, стимулировавшей развитие представленной системы визуализации, была проблема визуального исследования максимальных стабильных мостов в линейных дифференциальных играх с двумерной эквивалентной фазовой переменной. В настоящее время численно исследуется задача преследования-уклонения с двумя догоняющими и одним убегающим объектом, предложенная в [7]. После специальной замены переменных эта задача позволяет сократить размерность фазового вектора до 2 и использовать разработанную систему трехмерной визуализации.

В данной задаче интерес для исследования представляют пропадание бесконечных частей множеств; наличие негладкостей на поверхности множеств; потеря односвязности сечениями, перпендикулярными оси t.

Для решения данной задачи был создан соответствующий фильтр. Примеры работы фильтра приведены на рис. 2, 5 и 10.

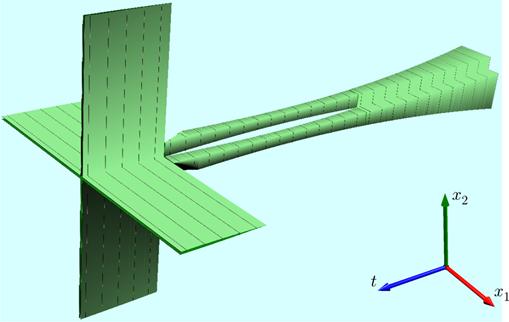
image description

Рис. 10. Трехмерный вид объектов, исследуемых в рамках задачи преследовния.

4.3. Другие задачи.

Разработанная система также используется и тестируется авторами в рамках ряда других исследований. В настоящее время создаются и отрабатываются модули двух- и трехмерной визуализации графов, изображения сложных многогранников, составленных из параллелепипедов, наглядного представления преобразований комплексной плоскости. В рамках этих работ изучаются, во-первых, имеющиеся изобразительные и манипуляционные возможности системы; во-вторых, качество программного интерфейса, предоставляемого ядром; в-третьих, при недостатке возможностей системы продумываются те инструменты, которые разумно было бы добавить.

5. Заключение.

В статье описан создаваемый авторами конструктор специализированных систем визуализации. Главной особенностью проекта является его модульная структура: все алгоритмы восстановления трехмерных объектов отображаемой сцены вынесены из программы и оформляются в виде внешних DLL-библиотек, скриптов или программ. Это позволяет относительно легко расширять круг отображаемых объектов, создавая на том или ином подходящем языке программирования соответствующие процедуры, ориентированные на конкретные форматы числовых данных и формы их визуального представления.

Таким образом, разработка новой системы визуализации из сложного проекта, включающего в себя множество рутинных технических задач, превращается в процесс адаптации, использования и расширения возможностей предложенного конструктора систем визуализации.

Информация по развитию среды визуализации публикуется авторами в сети Интернет на сайте: http://www.sharpeye.lact.ru

Среди ближайших планов по развитию системы – реализация анимации и редактируемой истории манипуляций (undo/redo).

Литература

1. Авербух В.Л., Юртаев Д.Ю. Методика разработки специализированных систем визуализации на примере задачи построения мостов в линейных дифференциальных играх // Алгоритмы и программные средства параллельных вычислений: Сб. науч. тр. / Екатеринбург. ИММ УрО РАН 1998. Вып.2, Екатеринбург, ИММ УрО РАН, 1998, С.3-9.

2. Averbukh V.L., Kumkov S.S., Patsko V.S., Pykhteev O.A., Yurtaev D.A. Specialized Visualization Systems for Differential Games // Progress in Simulation, Modeling, Analysis and Synthesis of Modern Electrical and Electronic Devices and Systems, N.E.Mastorakis (Ed.), WSES Press, 1999, pp.301-306.

3. Averbukh V.L., Kumkov S.S., Shilov E.A., Yurtaev D.A., Zenkov A.I. Specialized Scientific Visualization Systems for Optimal Control Application // A Proceedings Volume from the IFAC Workshop on Nonsmooth and Discontinuous Problems of Control and Optimization, Chelyabinsk, Russia, 17-20 June 1998, Batukhtin V.D., Kirillova F.M., Ukhobotov V.I. (Eds.), Pergamon Press, Great Britain, 1999, pp.28-33.

4. Averbukh V.L., Ismagilov T.R., Patsko V.S., Pykhteev O.A., Turova V.L. Vizualization of Value Function in Time-Optimal Differential Games // Proceedings of the 15th Conference on Scientific Computing "ALGORITMY 2000", Vysoke Tatry – Podbanske, Slovakia, September 10-15, 2000, Handlovicova A., Komornikova M., Mikula K., Sevcovic D. (Eds.), Slovak University of Technology, Bratislava Faculty of Civil Engineering Department of Mathematics and Descriptive Geometry, 2000, pp. 207-216.

5. Зенков А.И. Разработка подхода к созданию специализированных систем визуализации для высокопроизводительных научных вычислений // Вопросы атомной науки и техники. Серия: Математическое моделирование физических процессов, Вып.4, 2003, С.81-86.

6. Brykalov, S.A., Lebedev, P.D., Uspenskii, A.A., Ushakov, A.V. Symmetry Sets in Construction of a Minimax Solution for a Bellman-Isaacs Equation, Proceedings of the 18th IFAC World Congress, Edited by S. Bittanti, A. Cenedese, S. Zampieri, Milan, 2011, Vol. 18, Part 1, IFAC PapersOnLine Identifier: 10.3182/20110828-6-IT-1002.00744.

7. Le Menec S. Linear differential game with two pursuers and one evader // Annals of the International Society of Dynamic Games, Vol.11: Advances in Dynamic Games. Theory, Applications, and Numerical Methods for Differential and Stochastic Games, Boston: Birkhauser, 2011, pp.209-226.

Extensible Scientific Visualization System

P. Vasev¹, S. Kumkov^1,2, E. Shmakov²

¹Institute of Mathematics and Mechanics UrB RAS, Ekaterinburg, Russia

²Ural Federal University, Ekaterinburg, Russia

sskumk@gmail.com

Abstract

The paper describes scientific visualization system which is being developed by the authors. Scientific visualization is meant as an approach for converting abstract objects to some geometric figures which allows a researcher to observe results of numerical simulation. Thus, the visualization chain consists of a computational program, which produces numerical data, a procedure of generating geometric figures on the basis of this data and an environment to manipulate the scene containing these figures. The main peculiarity of the system suggested by the authors is the support of any data format and its visual representations. This is gained by providing rich application programming interface (API) to control the scene: for geometric objects, light sources, cameras, history of actions, etc. It allows developing new individual procedure for creating geometric objects for each new data format, suitable to the demands of the researcher. The system is written in C# for the Windows .NET 4.0 environment. The system allows to specify user procedures for creating visual objects within .NET DLLs, Ruby scripts and console applications. The paper is concluded by examples of successfully solved problems using the system.

Keywords: scientific visualization, visualization system, visualization framework, user-defined visual representation, visual analytics.

References

1. Averbukh V.L., YUrtaev D.YU. Metodika razrabotki spetsializirovannykh sistem vizualizatsii na primere zadachi postroeniya mostov v lineynykh differentsialnykh igrakh [Methods of development of specialized imaging systems for the problem of building bridges in linear differential games]. Algoritmy i programmnye sredstva parallelnykh vychisleniy: Sb. nauch. tr. [Algorithms and software for parallel computing] Ekaterinburg: IMM UrO RAN, 1998, vol. 2, pp. 3-9.

2. Averbukh V.L., Kumkov S.S., Patsko V.S., Pykhteev O.A., Yurtaev D.A. Specialized Visualization Systems. for Differential Games Progress in Simulation, Modeling, Analysis and Synthesis of Modern Electrical and Electronic Devices and Systems, N.E.Mastorakis (Ed.), WSES Press, 1999, pp.301-306.

3. Averbukh V.L., Kumkov S.S., Shilov E.A., Yurtaev D.A., Zenkov A.I. Specialized Scientific Visualization Systems for Optimal Control Application. A Proceedings Volume from the IFAC Workshop on Nonsmooth and Discontinuous Problems of Control and Optimization, Chelyabinsk, Russia, 17-20 June 1998, Batukhtin V.D., Kirillova F.M., Ukhobotov V.I. (Eds.), Pergamon Press, Great Britain, 1999, pp.28-33.

4. Averbukh V.L., Ismagilov T.R., Patsko V.S., Pykhteev O.A., Turova V.L. Vizualization of Value Function in Time-Optimal Differential Games. Proceedings of the 15th Conference on Scientific Computing "ALGORITMY 2000", Vysoke Tatry – Podbanske, Slovakia, September 10-15, 2000, Handlovicova A., Komornikova M., Mikula K., Sevcovic D. (Eds.), Slovak University of Technology, Bratislava Faculty of Civil Engineering Department of Mathematics and Descriptive Geometry, 2000, pp. 207-216.

5. Zenkov A.I. Razrabotka podkhoda k sozdaniyu spetsializirovannykh sistem vizualizatsii dlya vysokoproizvoditelnykh nauchnykh vychisleniy [Develop an approach to the creation of specialized imaging systems for high performance scientific computing]. Voprosy atomnoy nauki i tekhniki. Seriya: Matematicheskoe modelirovanie fizicheskikh protsessov [Problems of Atomic Science and Technology. Series: Mathematical modeling of physical processes], Sarov: VNIEF, 2003, vol. 4, pp. 81-86.

6. Brykalov, S.A., Lebedev, P.D., Uspenskii, A.A., Ushakov, A.V. Symmetry Sets in Construction of a Minimax Solution for a Bellman-Isaacs Equation. Proceedings of the 18th IFAC World Congress, Edited by S. Bittanti, A. Cenedese, S. Zampieri, Milan, 2011, Vol. 18, Part 1, IFAC PapersOnLine Identifier: 10.3182/20110828-6-IT-1002.00744.

7. Le Menec S. Linear differential game with two pursuers and one evader. Annals of the International Society of Dynamic Games, Advances in Dynamic Games. Theory, Applications, and Numerical Methods for Differential and Stochastic Games, Vol.11: Boston: Birkhauser, 2011, pp.209-226.